1 问题
给定一个单链表的头节点 head,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
本题中,一个
高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差不超过 1。
示例 1
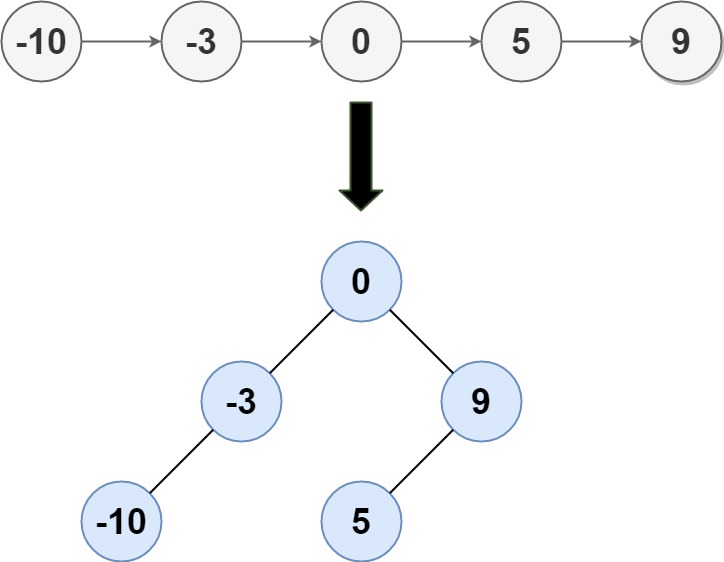
示例1
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2
输入: head = []
输出: []
提示
- head中的节点数在[0, 2 * 104]范围内
- -105<= Node.val <= 105
2 解题思路
单链表、二叉树结构:
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}不同于【LeetCode】108.将有序数组转换为二叉搜索树 ,本题中已知输入为
有序链表,但思想还是一样的。2.1 递归 + 快慢指针
数组可以根据下标快速定位左右子树的范围,对于链表,我们同样可以利用指针来划分,原理就是快慢指针。
快指针速度是慢指针的两倍,等到快指针到底链表末尾或者为null,慢指针刚好位于中间节点。
算法过程:
- 假定
head为链表头结点,slow表示慢指针,fast表示快指针; - 起始状态:
slow=head; fast=head.next.next;; - 只要
null != fast且null != fast.next,则循环执行slow = slow.next; fast = fast.next.next;; - 执行完上一步的循环,此时
slow的下一个节点即为链表中点,则以该中点为根节点root,root左子树范围为[head, slow],其右子树范围为[slow.next.next, 链表结尾]; - 上述结论用已知的构造方法表示为:
root.left = sortedListToBST(head); root.right = sortedListToBST(slow.next.next);
2.2 递归 + 中序遍历
学习了k神的思想,觉得真是🐂🍺,上述算法存在的问题时,每次递归都需要重新遍历节点找出根节点,左右子树范围,效率略低。k神的算法就是想减少循环遍历,通过一次遍历链表的过程,来构造题目要求的高度平衡二叉搜索树。
大致流程:
- 使用
递归模拟中序遍历过程,建立节点的顺序即与链表元素顺序一一对应,bottom-up(自底向上)建立树,最终返回根节点。 - 递归前需要统计链表长度
n,整体算法复杂度O(N)。
3 代码
3.1 递归 + 快慢指针
class Solution {
public TreeNode sortedListToBST(ListNode head) {
//null
if (null == head) {
return null;
}
//single node
if (null == head.next) {
return new TreeNode(head.val);
}
//严格递增,二分法
//快慢指针找到中间节点,一分为二
//给定一个空的头结点,方便
ListNode dummy = new ListNode(-1);
dummy.next = head;
ListNode slow = dummy;
ListNode fast = dummy.next.next;
while (null != fast && null != fast.next) {
slow = slow.next;
fast = fast.next.next;
}
//此时 slow位于中间节点的上一节点
//准备拆分
//中间节点为根节点
TreeNode root = new TreeNode(slow.next.val);
//中间节点的下一节点为右子树部分
ListNode rightPart = slow.next.next;
//此处截断,左子树范围[head, slow],剩下的除root外,全是右子树的范围
slow.next = null;
//left tree
root.left = sortedListToBST(dummy.next);
//right tree
root.right = sortedListToBST(rightPart);
return root;
}
}3.2 递归 + 中序遍历
class Solution {
ListNode newNode;
public TreeNode sortedListToBST(ListNode head) {
//null
if (null == head) {
return null;
}
//single node
if (null == head.next) {
return new TreeNode(head.val);
}
int n = 0;
newNode = head;
while (null != head) {
head = head.next;
n++;
}
return build(0, n - 1);
}
private TreeNode build(int left, int right) {
if (left > right) {
return null;
}
//middle
int mid = left + (right - left) / 2;
//inorder traversal
//left tree
TreeNode leftTree = build(left, mid - 1);
//root,此时,再构造完左子树后,newNode已经是链表的中点节点了
TreeNode root = new TreeNode(newNode.val);
newNode = newNode.next;
root.left = leftTree;
root.right = build(mid + 1, right);
return root;
}
}注:LC108/LC109构造结果不唯一,比如[-10,-3,0,5,9],可以构造出以下
高度平衡的二叉搜索树:
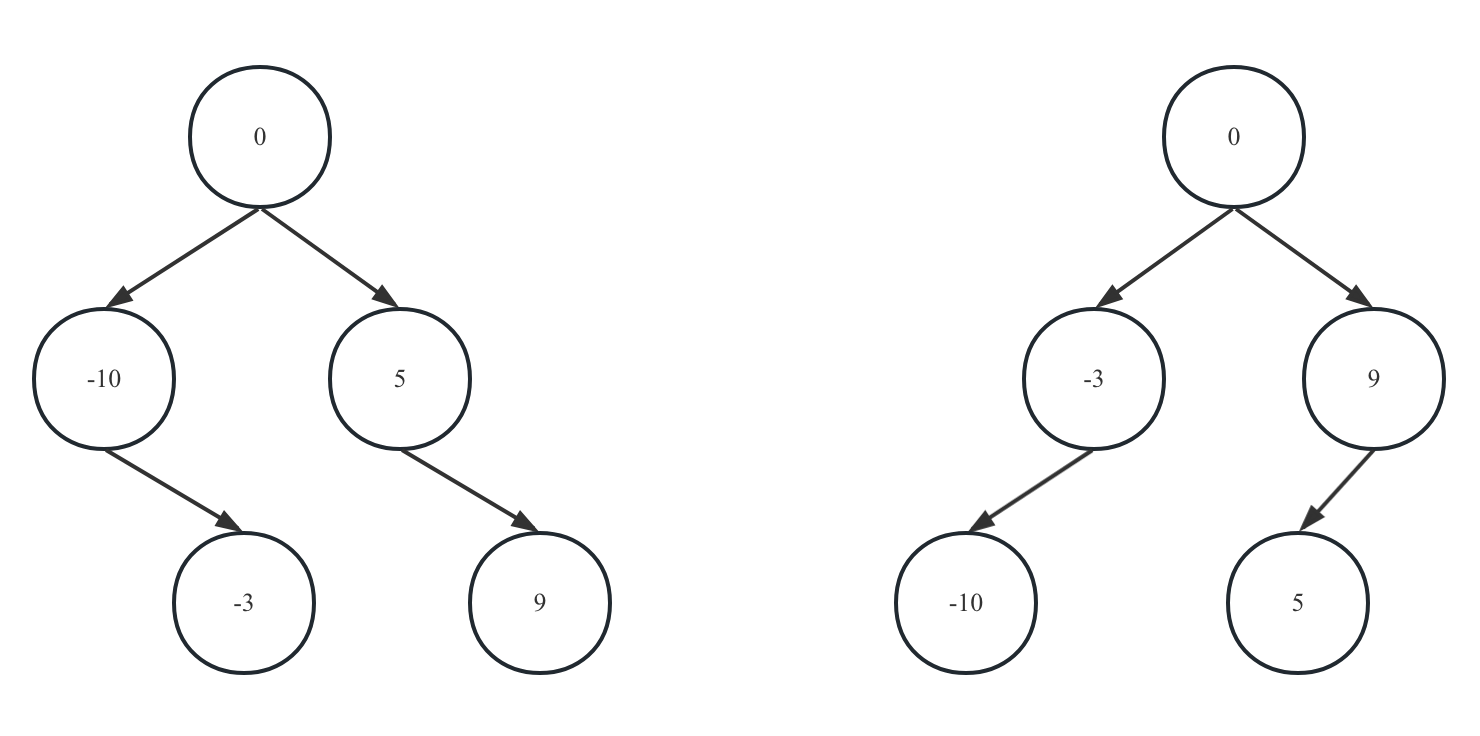
两颗不同的高度平衡二叉搜索树



