1 问题
给定一个二叉树的根节点 root,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1
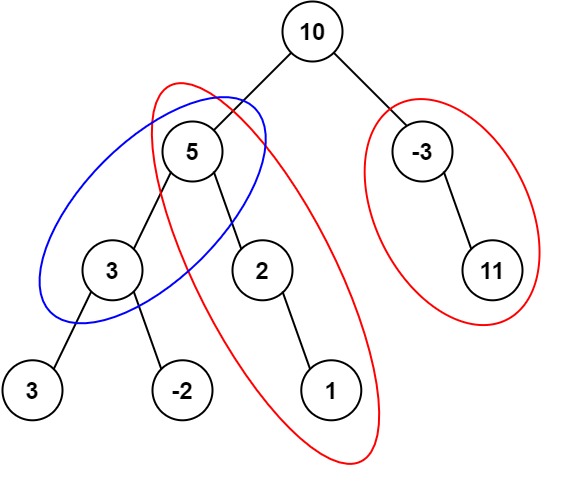
示例1
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。示例 2
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示
二叉树的节点个数的范围是 [0,1000]
- -109<= Node.val <= 109
- -1000<= targetSum<= 1000
2 解题思路
- 这一题是第 112 题和第 113 题的加强版,这一题要求求出任意一条路径的和为
sum,起点不一定是根节点,可以是任意节点开始。 - 注意这一题可能出现负数的情况,节点和为 sum,并不一定是最终情况,有可能下面还有正数节点和负数节点相加正好为 0,那么这也是一种情况。一定要遍历到底。
- 一个点是否为
sum的起点,有3 种情况:- 第一种情况:路径包含该
root节点,如果包含该结点,就在它的左子树和右子树中寻找和为sum-root.val的情况。 - 第二、三种情况:路径不包含该
root节点,那么就需要在它的左子树或右子树中分别寻找和为sum的结点。
- 第一种情况:路径包含该
总结起来就是:结果包含根到子节点的路径之和等于targetSum、子节点与其子节点的路径之和等于targetSum。
3 代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if (null == root) {
return 0;
}
//results include root-leaf and subtree
//with root
int cnt = pathFromRoot(root, targetSum);
//without root
cnt += pathSum(root.left, targetSum);
cnt += pathSum(root.right, targetSum);
return cnt;
}
/**
*
* @param root
* @param target
* @return res
* @description
* 对于用例 root = [1000000000,1000000000,null,294967296,null,1000000000,null,1000000000,null,1000000000]
* 调用递归的时候传入的参数是targetSum-root.val,这里root.val太大了,递归调用多了targetSum-root.val就会溢出整数型的最小值。
* 把参数类型换成long即可。
*/
private int pathFromRoot(TreeNode root, long target) {
if (null == root) {
return 0;
}
int res = 0;
if (target == root.val) {
res++;
}
//left subtree
res += pathFromRoot(root.left, target - root.val);
//right subtree
res += pathFromRoot(root.right, target - root.val);
return res;
}
}


