1.问题
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
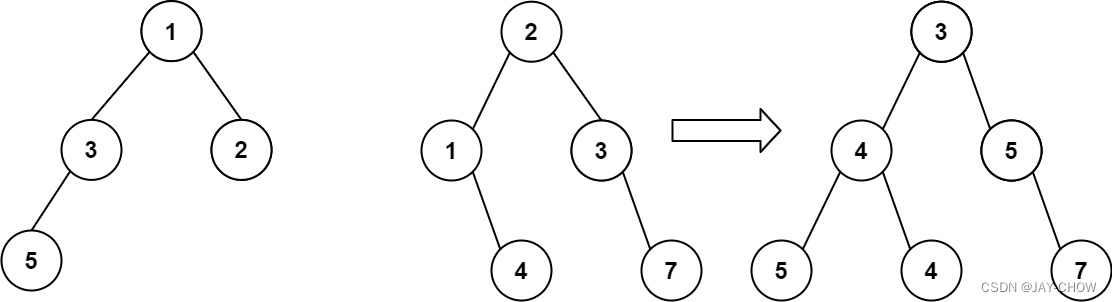
示例 1
""
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
提示:
- 两棵树中的节点数目在范围 [0, 2000] 内
- -104 <= Node.val <= 104
2.解题思路
2.1 递归
采用前序遍历方式,遍历两颗树,对于单个节点,存在以下三种情况进行合并处理: - 如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
- 如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
- 如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,此时需要显性合并两个节点
处理完单个节点后,还要对节点的左右子树进行处理,因而递归。可以拿root1为主干。参考代码中递归算法的实现。
复杂度:
- 时间复杂度:O(N)
- 空间复杂度:O(h),h 是树的高度
2.2 迭代
还是以root1为主干进行合并,利用层次遍历的方法,对于同时非空的左节点或右节点进行合并,若root1的left为空,则将root2.left赋值给root1.left;同理,若root1.right为空,则将root2.right赋值给它。
复杂度:
- 时间复杂度:O(N)
- 空间复杂度:O(N),对于满二叉树时,要保存所有的叶子节点,即 N/2 个节点。
3.代码
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { //递归解法(DFS) public TreeNode mergeTrees(TreeNode root1, TreeNode root2) { //空节点处理 if(null==root1 || null== root2){ return null!=root2?root2:root1; } root1.val+=root2.val; root1.left=mergeTrees(root1.left, root2.left); root1.right=mergeTrees(root1.right, root2.right); return root1; } //迭代(BFS) public TreeNode mergeTrees(TreeNode t1, TreeNode t2) { //如果 t1和t2中,只要有一个是null,函数就直接返回 if(t1==null || t2==null) { return t1==null? t2 : t1; } Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(t1); queue.offer(t2); while(queue.size()>0) { TreeNode r1 = queue.poll(); TreeNode r2 = queue.poll(); r1.val += r2.val; //如果r1和r2的左子树都不为空,就放到队列中 //如果r1的左子树为空,就把r2的左子树挂到r1的左子树上 if(r1.left!=null && r2.left!=null){ queue.offer(r1.left); queue.offer(r2.left); } else if(r1.left==null) { r1.left = r2.left; } //对于右子树也是一样的 if(r1.right!=null && r2.right!=null) { queue.offer(r1.right); queue.offer(r2.right); } else if(r1.right==null) { r1.right = r2.right; } } return t1; } }


