1 空间直线的一般方程
两平面的交线
2 空间直线的对称式(点向式)方程
直线的方向向量:$\overrightarrow{s}=(m,n,p)$
直线上的一点:$M_0(x_0,y_0,z_0)$
对称式方程:
3 空间直线的参数方程
由对称式方程:
得其参数方程:
4 两直线的夹角
直线$L_1$方向向量:$\overrightarrow{s_1}=(m_1,n_1,p_1)$,
直线$L_2$方向向量:$\overrightarrow{s_2}=(m_2,n_2,p_2)$,
夹角 $\phi \in [0,\frac{\pi}{2}]$
$cos \phi = \frac{|\overrightarrow{s_1} \cdot \overrightarrow{s_2}|}{|\overrightarrow{s_1}| \cdot |\overrightarrow{s_2}|} = \frac{|m_1m_2+n_1n_2+p_1p_2|}{\sqrt{m_1^2+n_1^2+p_1^2} \cdot \sqrt{m_2^2+n_2^2+p_2^2}}$
5 两直线垂直
$m_1m_2+n_1n_2+p_1p_2=0$
6 两直线平行或重合
$\frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{p_1}{p_2}$
7 直线与平面的夹角
$\phi \in [0,\frac{\pi}{2}]$
直线的方向向量:$\overrightarrow{s}=(m,n,p)$
$cos \theta = sin \phi = \frac{|Am+Bn+Cp|}{\sqrt{A^2+B^2+C^2} \cdot \sqrt{m^2+n^2+p^2}}$
8 平面束
8.1 定义
通过定直线的所有平面的全体。
设直线L由以下方程组确定:
其中,$A_1,B_1,C_1$与$A_2,B_2,C_2$不成比例,建立三元一次方程组
其表示通过直线L的所有平面。
9 点到直线的距离
设$M_0(x_0,y_0,z_0)$为直线L外任一点,$M(x_1,y_1,z_1)$为L上任一点,且L的方向向量$\overrightarrow{s}=(m,n,p)$,
则$M_0$到直线L的距离d:
$d=\frac{|\overrightarrow{M_0M} \times \vec{s}| }{|\vec{s}| }$
其中,$|\overrightarrow{M_0M} \times \vec{s}|$ 表示以$\overrightarrow{M_0M}$, $\vec{s}$为边的平行四边形的面积。
10 点到平面的距离
设$M_1(x_1,y_1,z_1)$为平面$\Pi$以外任一点,平面$\Pi$的方程为:
则,$M_1$到平面$\Pi$的距离公式:
$d=\frac{|Ax_1+By_1+Cz_1+D|}{\sqrt{A^2+B^2+C^2}}$
10.1 证明一
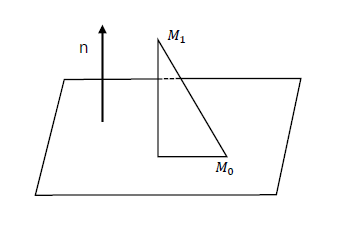
任取平面$\Pi$上一点$M_0(x_0,y_0,z_0)$,则其满足平面的方程
则$M_1$到平面$\Pi$的距离d即向量$\vec{M_0M_1}$在平面$\Pi$的法向量$\vec{n}$的投影大小。也就是:
$d=Prj_{\vec{n}}\overrightarrow{M_0M_1}=|\overrightarrow{M_0M_1}|\cos\phi=\frac{|\overrightarrow{M_0M_1} \cdot \vec{n}|}{|\vec{n}|}=\frac{|A(x_0-x_1)+B(y_0-y_1)+C(z_0-z_1)|}{\sqrt{A^2+B^2+C^2}}$
由于$Ax_0+By_0+Cz_0+D=0$,从而推出
10.2 证明二
通过求出$M_1$在平面$\Pi$的投影点$M_2$,然后算出$|\overrightarrow{M_2M_1}|$即可。
先求过$M_1$且垂直于平面$\Pi$的直线参数方程:
则$M_1$在平面$\Pi$的投影点$M_2$需要满足平面的方程:
即
再者,
将t带入上式即得:
$d=\frac{|Ax_1+By_1+Cz_1+D|}{\sqrt{A^2+B^2+C^2}}$



