1.问题
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,”ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
示例 2
输入:text1 = “abc”, text2 = “abc”
输出:3
解释:最长公共子序列是 “abc” ,它的长度为 3 。
示例 3
输入:text1 = “abc”, text2 = “def”
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
- 1 <= text1.length, text2.length <= 1000
- text1 和 text2 仅由小写英文字符组成。
2.解题思路
2.1 动态规划
定义dp~ij~表示text~1~的前i-1个字符和text~2~的前j-1个字符所能形成的最长公共子序列的长度。
令len1为text~1~的总长,len2为text~2~的总长,则dp~len1,len2~即为题目所求。 当 i=0 时,
text~1~ [0:i]为空,空字符串和任何字符串的最长公共子序列的长度都是 0,因此对任意0≤j≤len2,有dp~0,j~=0;当 j=0 时,
text~2~[0:j]为空,同理可得,对任意0≤i≤len1,有dp[i][0]=0。
因此动态规划的边界情况是:当 i=0 或 j=0 时,dp~i,0~=0。
当 i>0 且 j>0 时,考虑
dp~ij~的计算:当
text~1~[i−1] = text~2~[j−1]时,将这两个相同的字符称为公共字符,考虑text~1~[0:i−1]和text~2~[0:j−1]的最长公共子序列,再增加一个字符(即公共字符)即可得到text~1~[0:i]和text~2~[0:j]的最长公共子序列,因此dp~ij~=dp~i-1,j-1~+1。当
text~1~[i−1]≠text~2~[j−1]时,考虑以下两项:text~1~[0:i−1]和text~2~[0:j]的最长公共子序列;text~1~[0:i]和text~2~[0:j−1]的最长公共子序列。
要得到
text~1~[0:i]和text~2~[0:j]的最长公共子序列,应取两项中的长度较大的一项,因此dp~ij~ == max(dp~i−1,j~, dp~i,j−1~)。
由此可以得到如下状态转移方程:
- 当
text~1~[0:i-1]=text~2~[0:j-1],dp~i,j~ = dp~i-1,j-1~ +1; - 否则,dp~i,j~ =max{dp~i,j-1~ , dp~i-1,j~ }
最终,dp~len1,len2~ 即为text~1~ 和 text~2~ 的最长公共子序列。
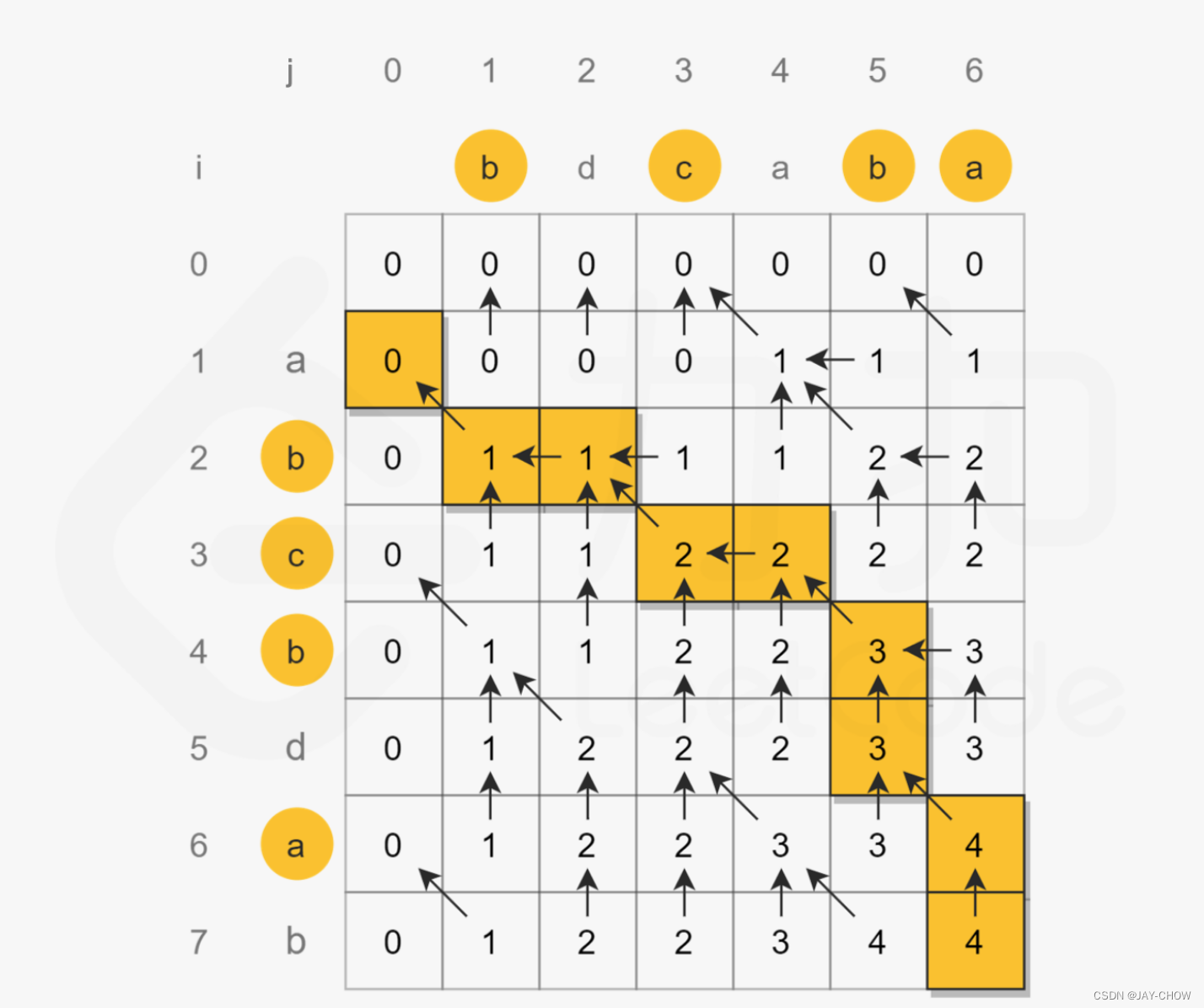
例如,text~1~ =abcddab, text~2~ =bdcaba,则动态规划矩阵如下图:
3.代码
class Solution {
/**
动态规划(利用偏移)
上述「追加空格」的做法是我比较习惯的做法 🤣
事实上,我们也可以通过修改「状态定义」来实现递推:
f[i][j] 代表考虑 s1 的前 i−1 个字符、考虑 s2 的前 j−1 的字符,形成的最长公共子序列长度。
那么最终的 f[n][m] 就是我们的答案,f[0][0] 当做无效值,不处理即可。
s1[i-1]==s2[j-1] : f[i][j]=f[i−1][j−1]+1。代表使用 s1[i−1] 与 s2[j−1] 形成最长公共子序列的长度。
s1[i-1]!=s2[j-1] : f[i][j]=max(f[i−1][j],f[i][j−1])。代表不使用 s1[i−1] 形成最长公共子序列的长度、不使用 s2[j−1] 形成最长公共子序列的长度。这两种情况中的最大值。
作者:宫水三叶
链接:https://leetcode.cn/problems/longest-common-subsequence/solutions/697187/gong-shui-san-xie-zui-chang-gong-gong-zi-xq0h/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
*/
public int longestCommonSubsequence(String text1, String text2) {
char[] t1 = text1.toCharArray();
char[] t2 = text2.toCharArray();
int length1 = t1.length;
int length2 = t2.length;
int[][] dp = new int[length1+1][length2+1];
for (int i = 1; i < length1 +1; i++) {
for (int j = 1; j < length2 +1; j++) {
if (t1[i-1] == t2[j-1]){
// 这边找到一个 lcs 的元素,继续往前找
dp[i][j] = 1+ dp[i-1][j-1];
}else {
//谁能让 lcs 最长,就听谁的
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[length1][length2];
}
}

