【LeetCode】145.二叉树的后续遍历

1.问题

给你一棵二叉树的根节点 root ，返回其节点值的 后序 遍历 。

示例 1

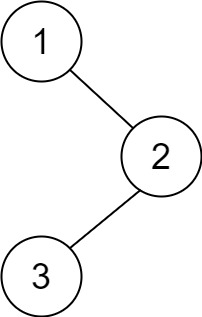
"图1"

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [1]
输出：[1]

提示：

• 树中节点的数目在范围 [0, 100] 内

• -100 <= Node.val <= 100

  2.解题思路

  二叉树的后序遍历规则：左-右-根，解题思路其实和前面两篇【LeetCode】144.二叉树的前序遍历差不太多.

  2.1 递归

  定义函数 postOrderTraversal(root)为遍历root节点。则调用顺序为：

  postOrderTraversal(root.left);
  postOrderTraversal(root.right);
  root.val;

  复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

2.2 迭代

1) 遍历root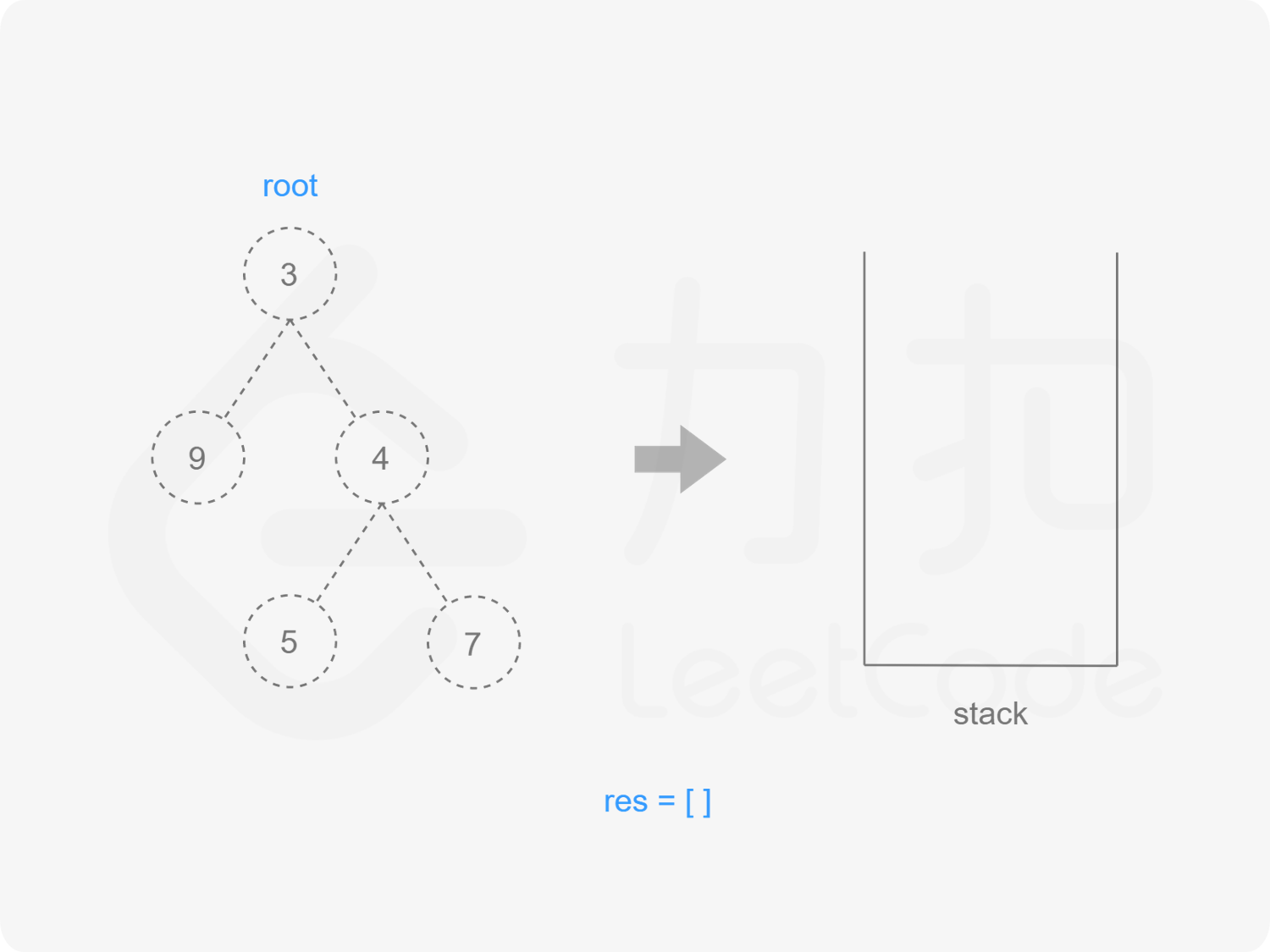

"图2"

2) root入栈

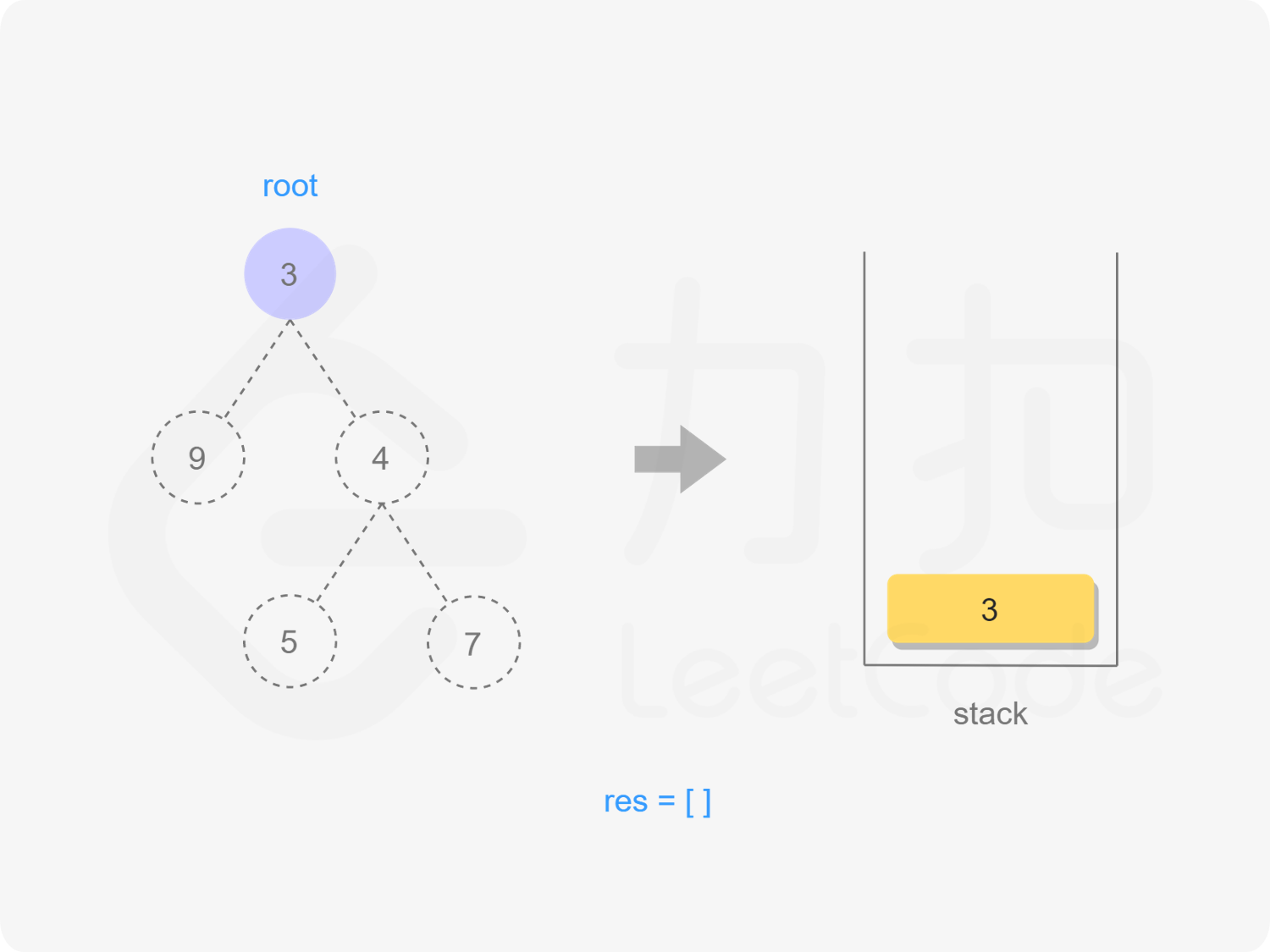
"图3"

3）root.left入栈

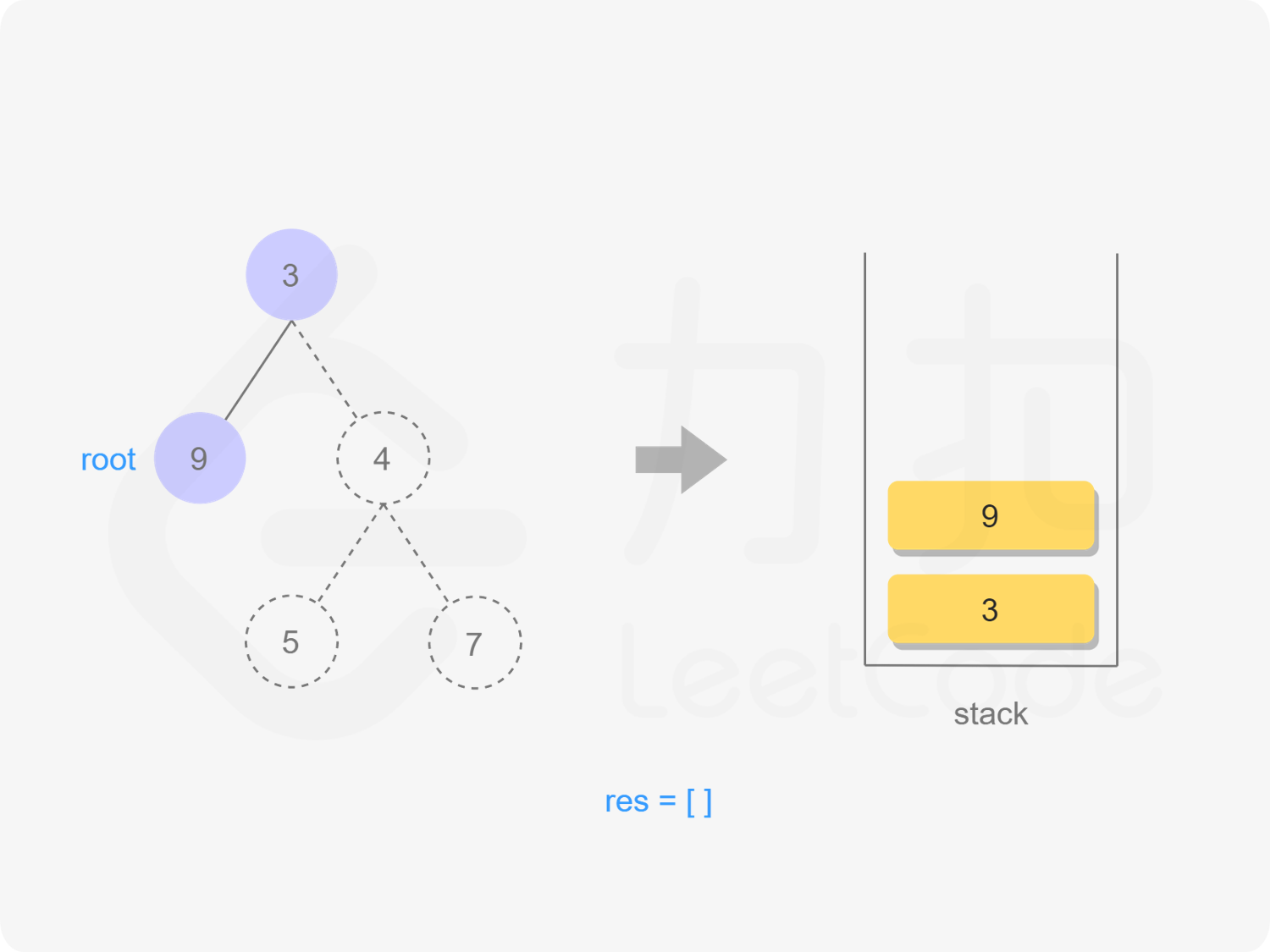
"图4"

4）root.left再无左子树了，左子树根节点出栈，遍历，并标记当前出栈的节点为已访问过，否则遍历、入栈root.right

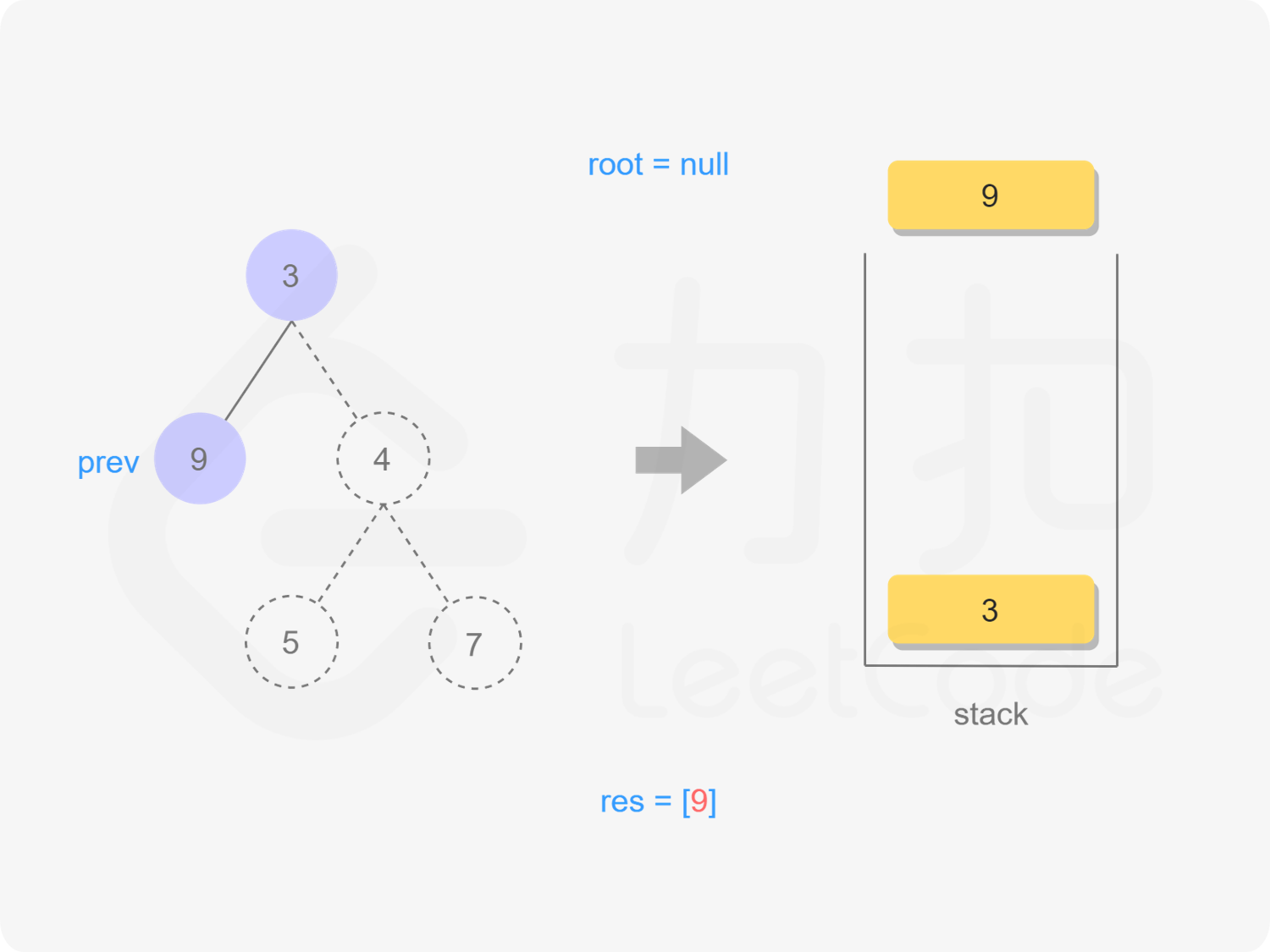
"图5"

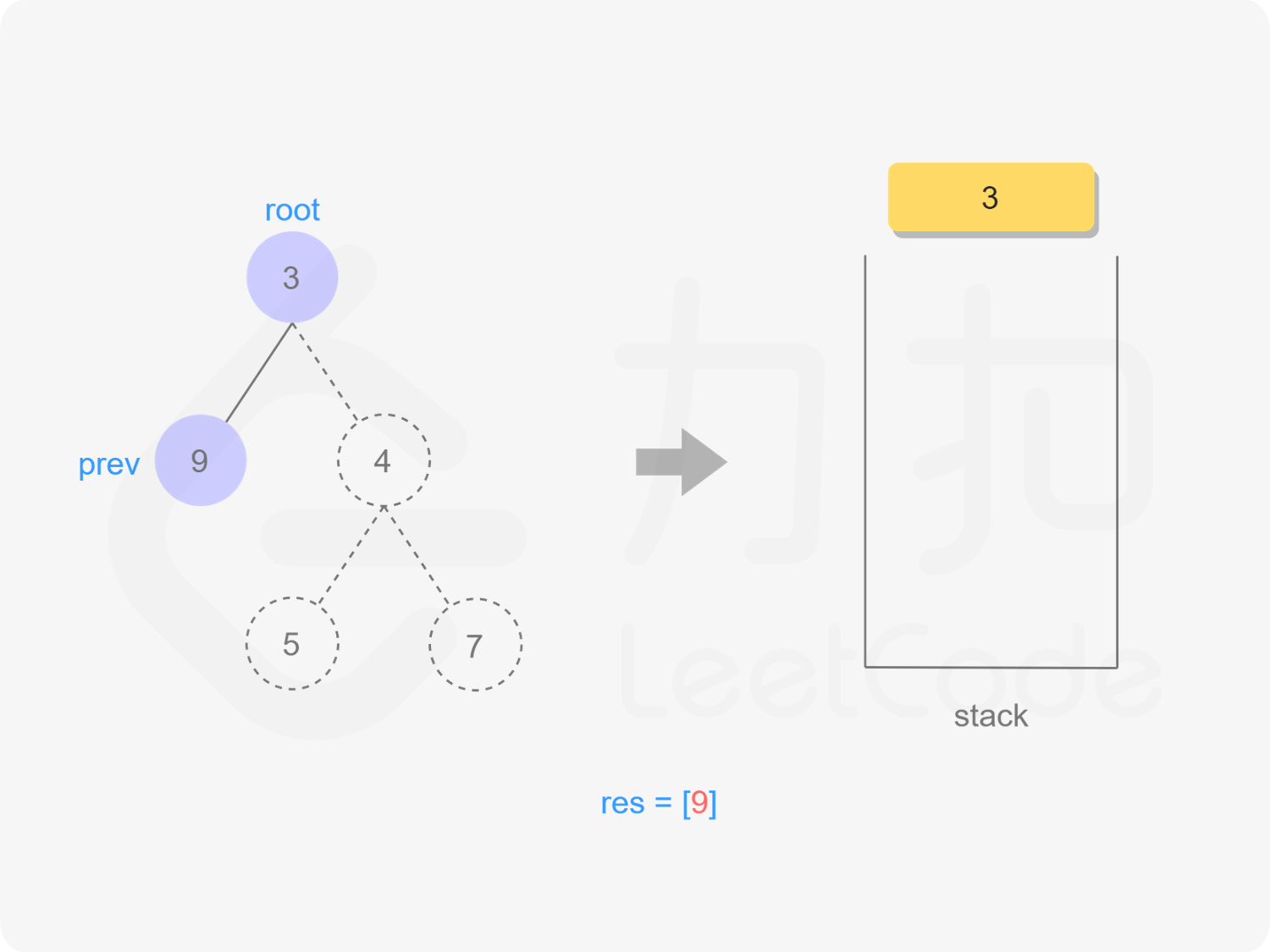
"图6"

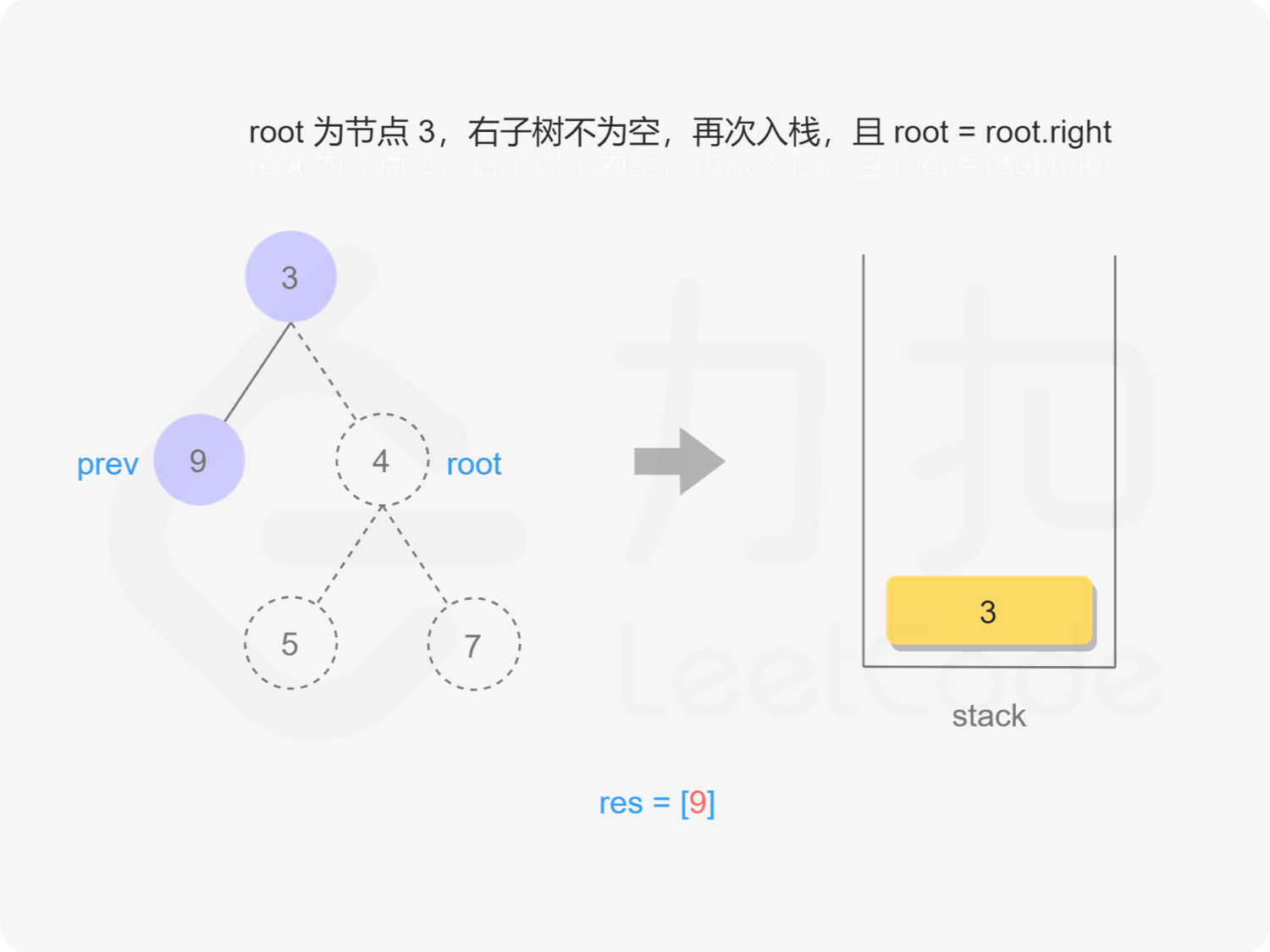
"图7"

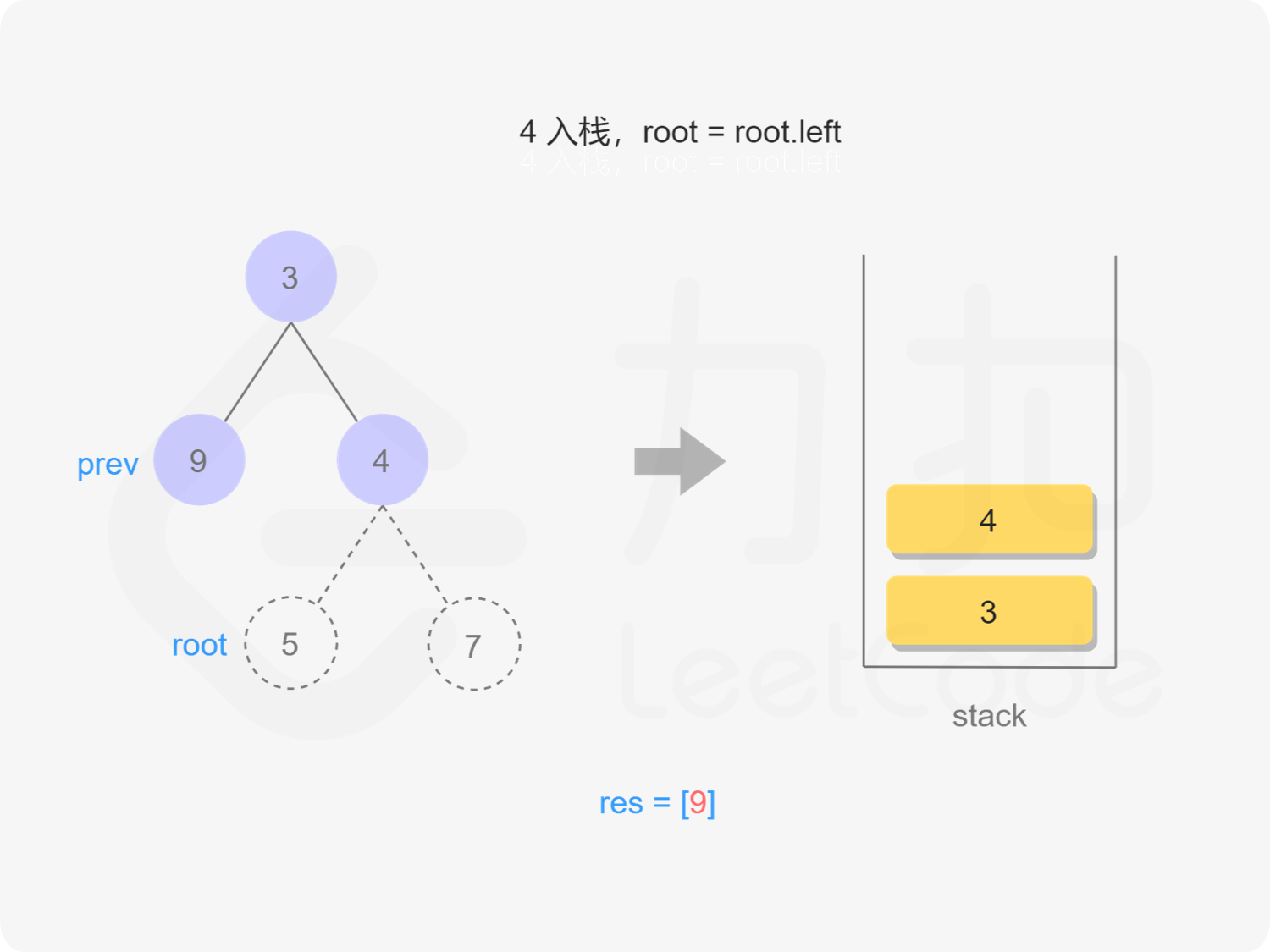
"图8"

5）同理，先把4所有左节点入栈，到达最左节点后，出栈，遍历val，标记当前出栈的节点为已访问过，遍历root.right，出栈root.right，root.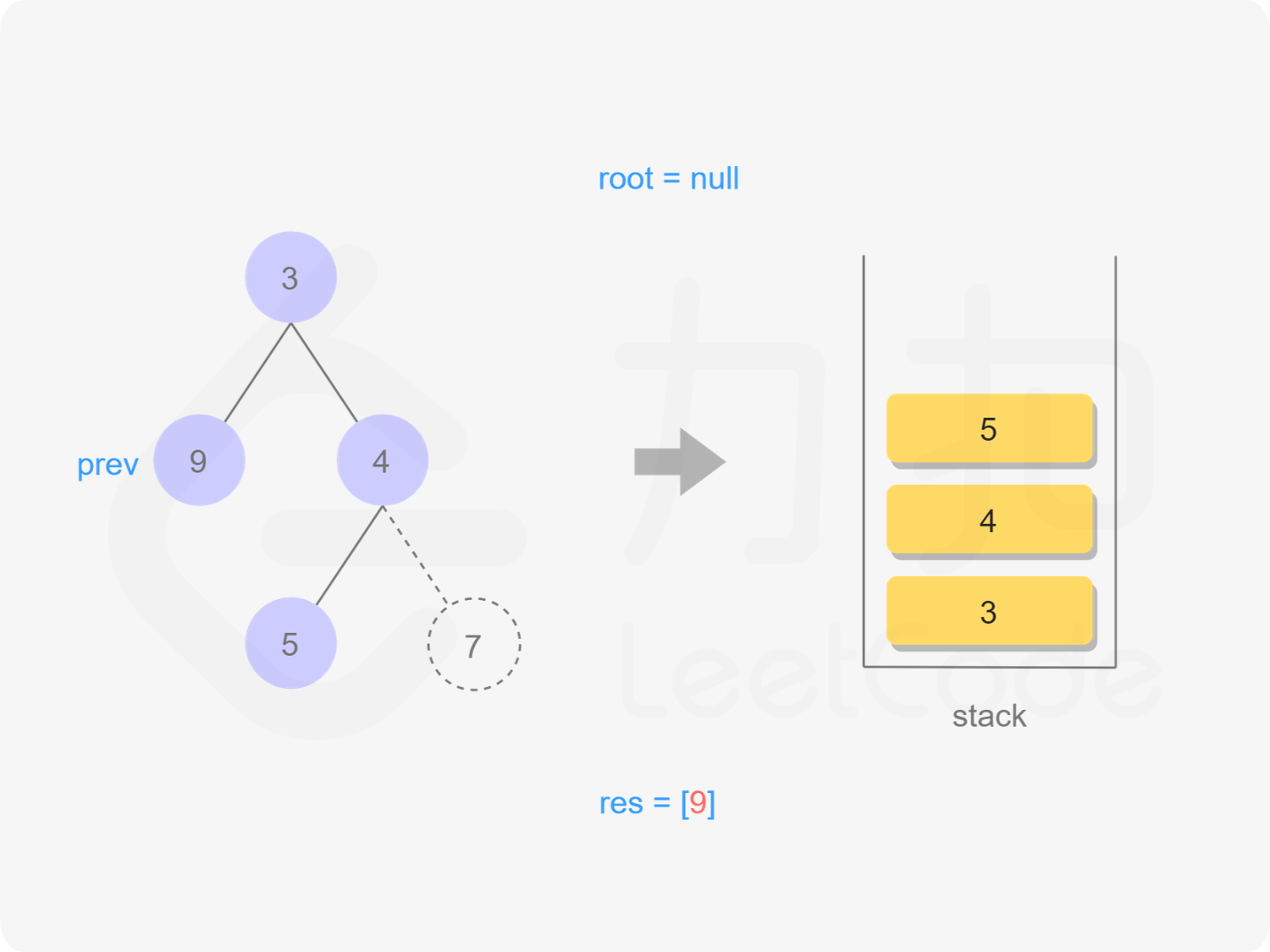

"图9"

5出栈

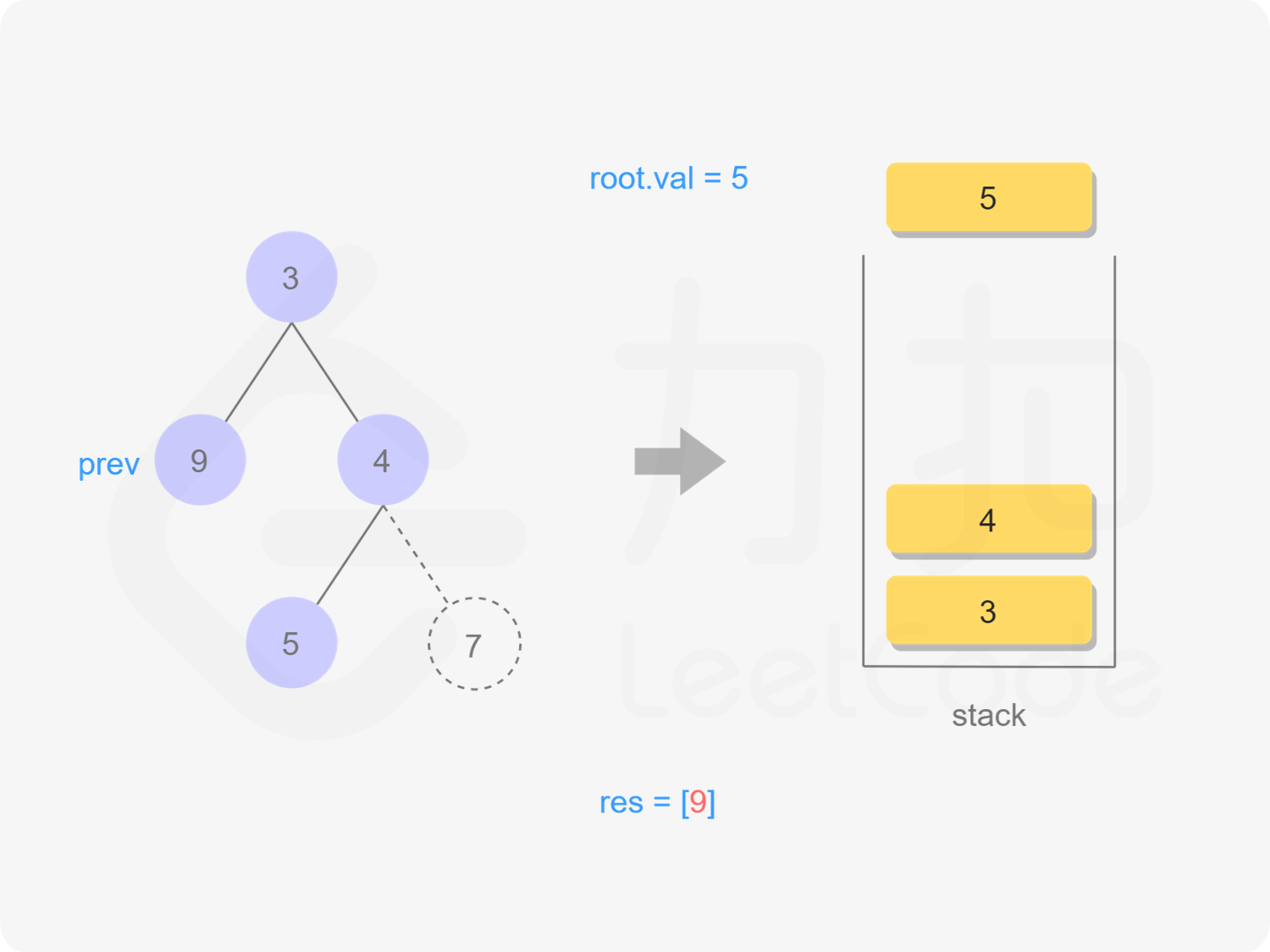
"图10"

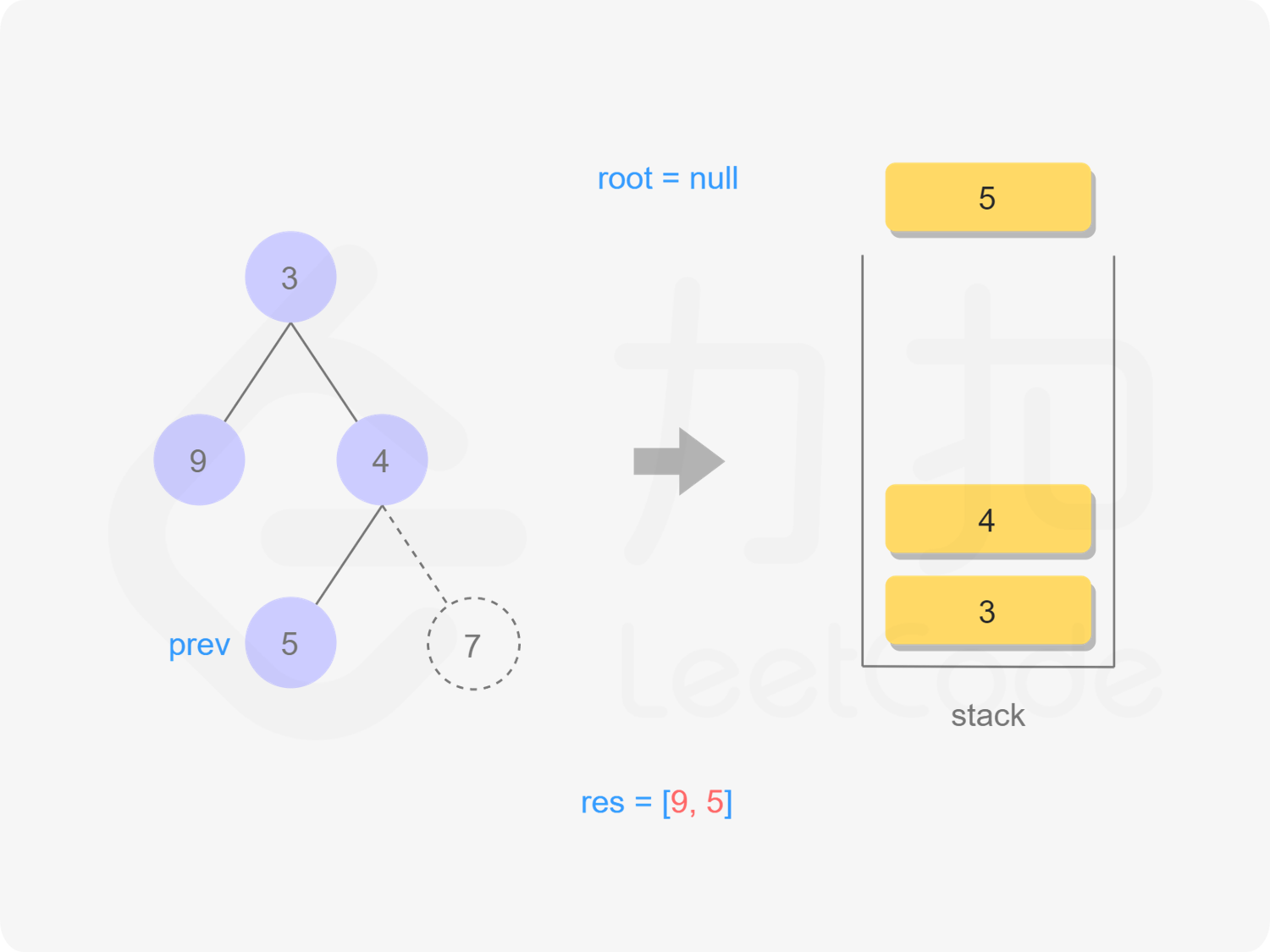
"图11"

4出栈，但4的右节点存在，入栈4.right

"图12"

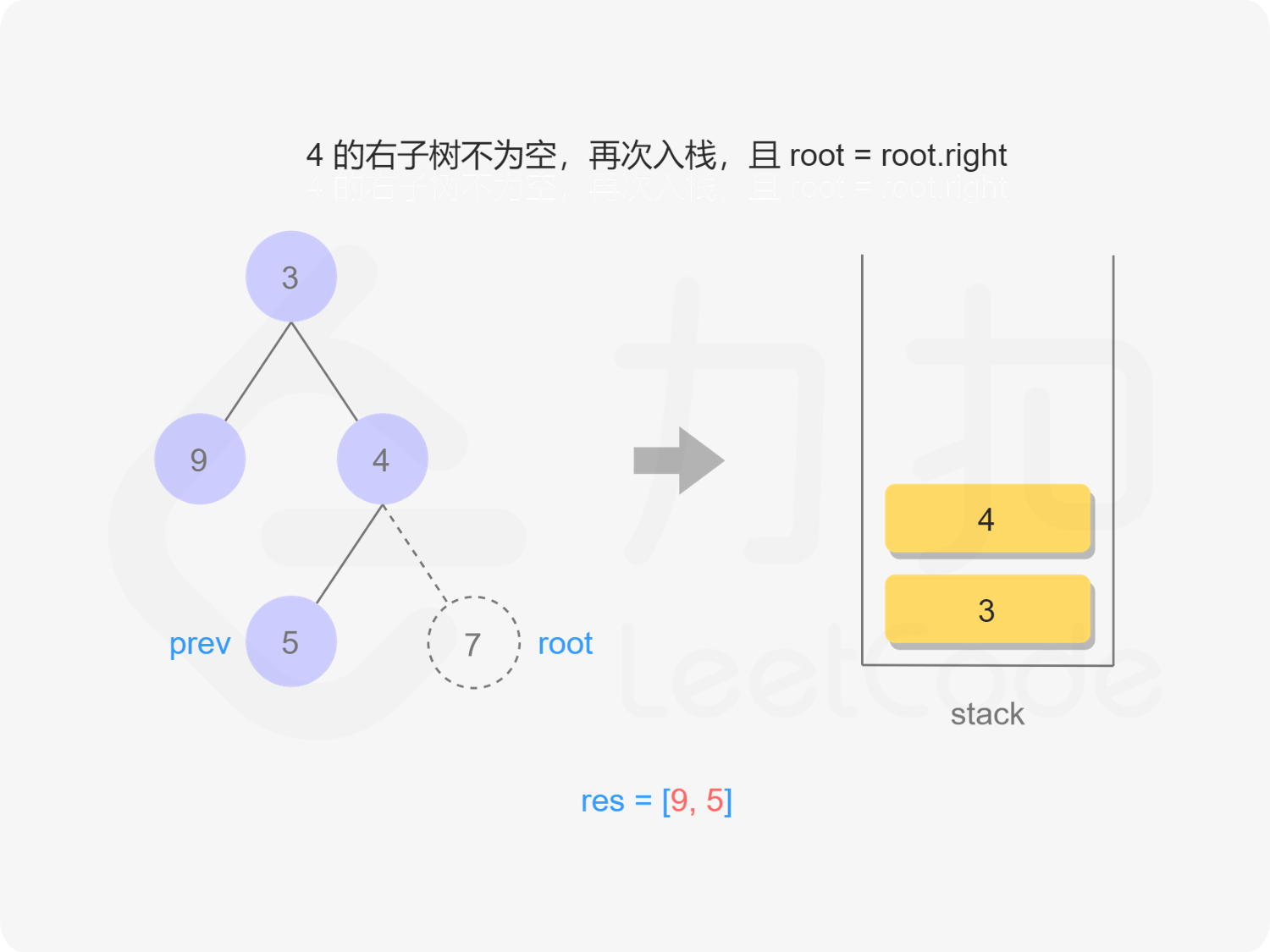
"图13"

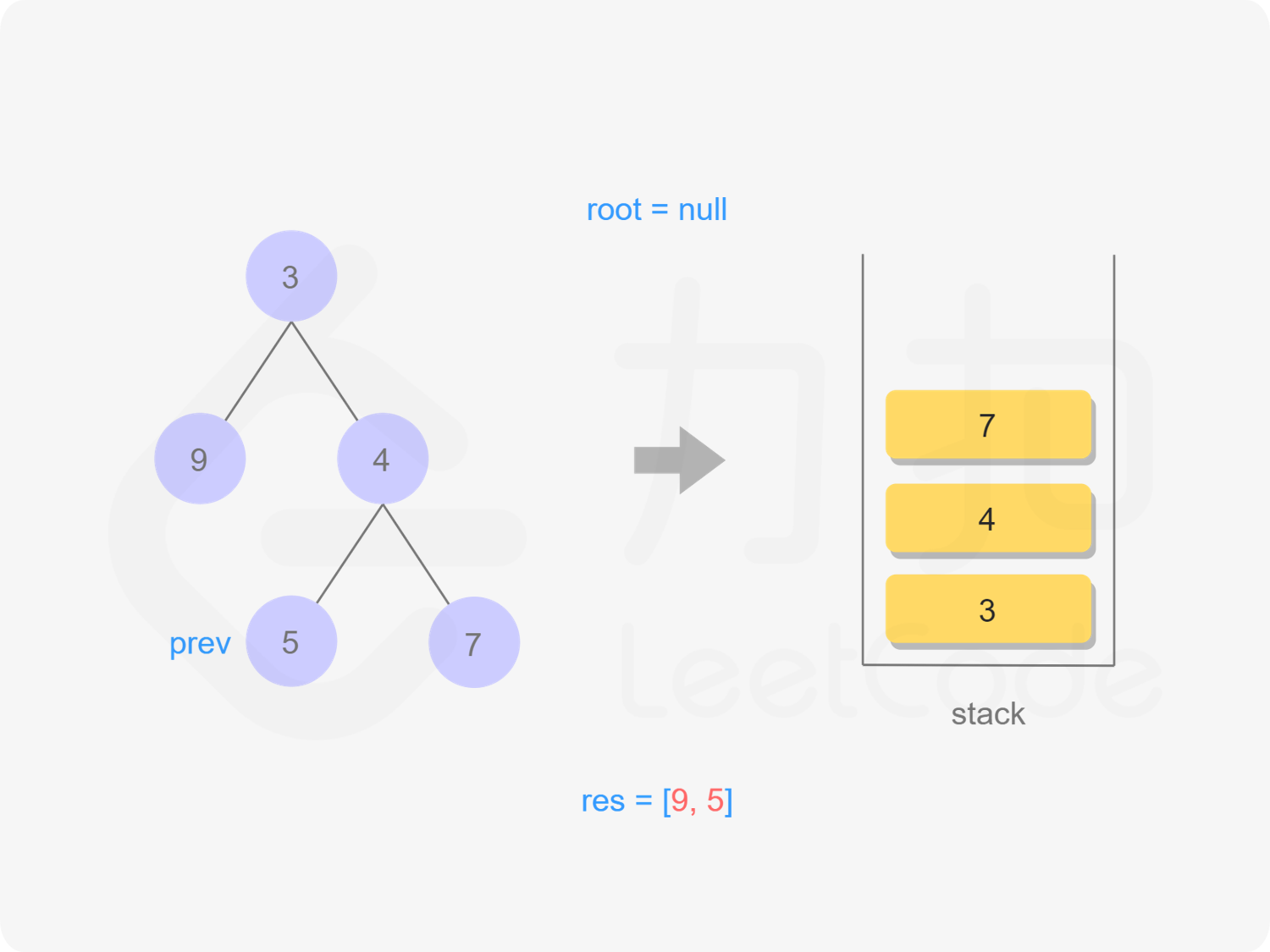
"图14"

7出栈，遍历，依次出栈4，3，遍历完毕

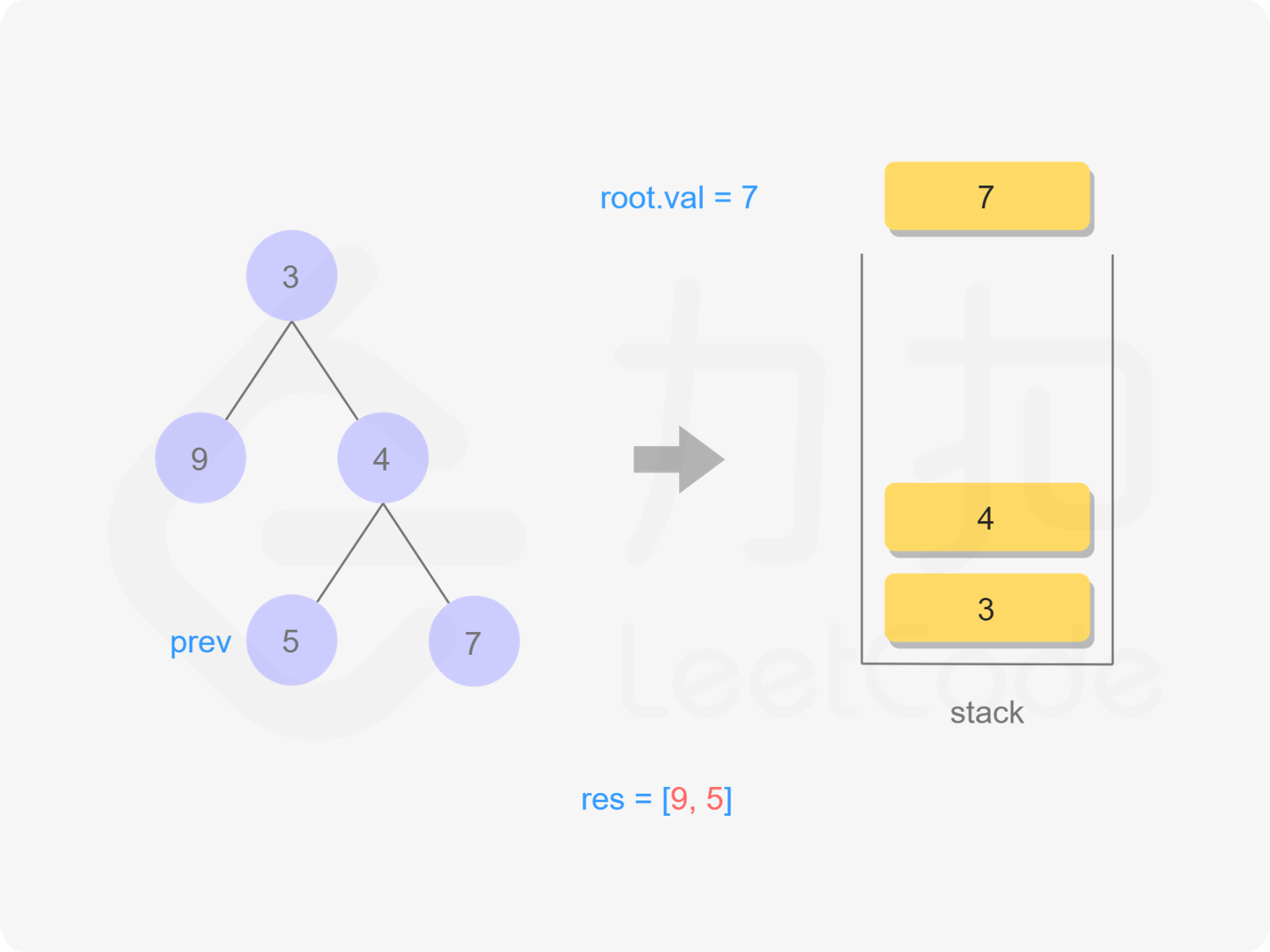
"图15"

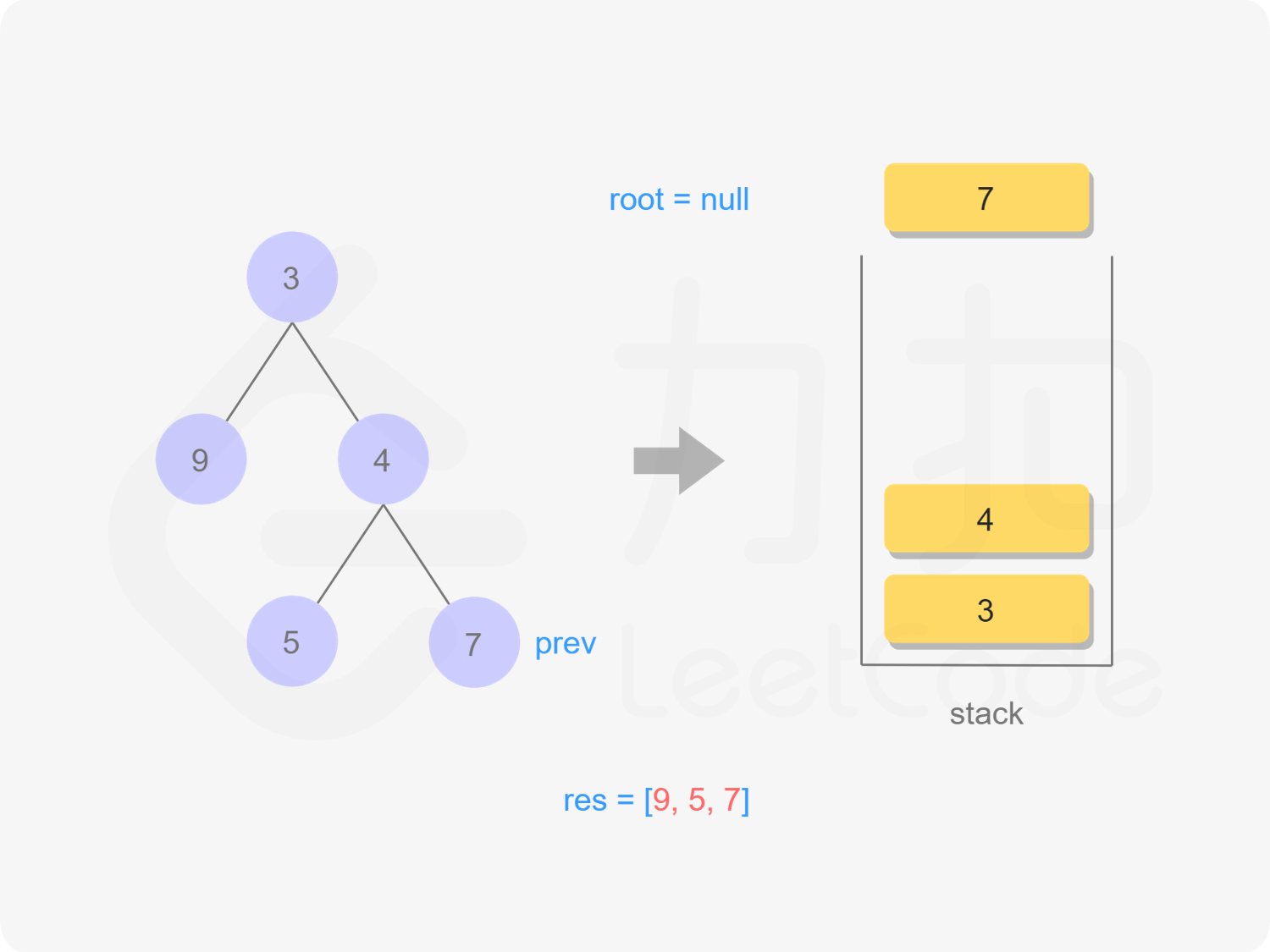
"图16"

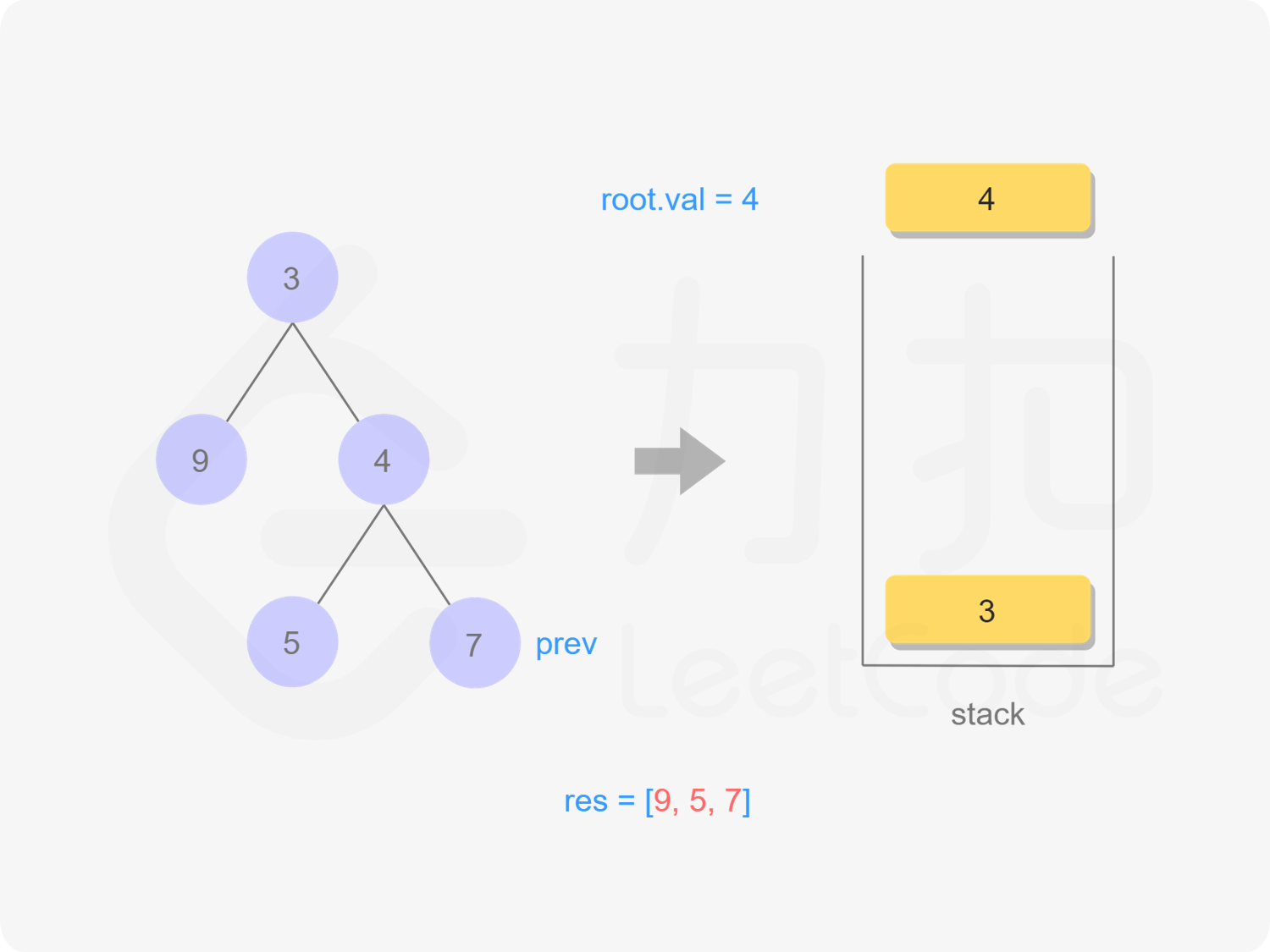
"图17"

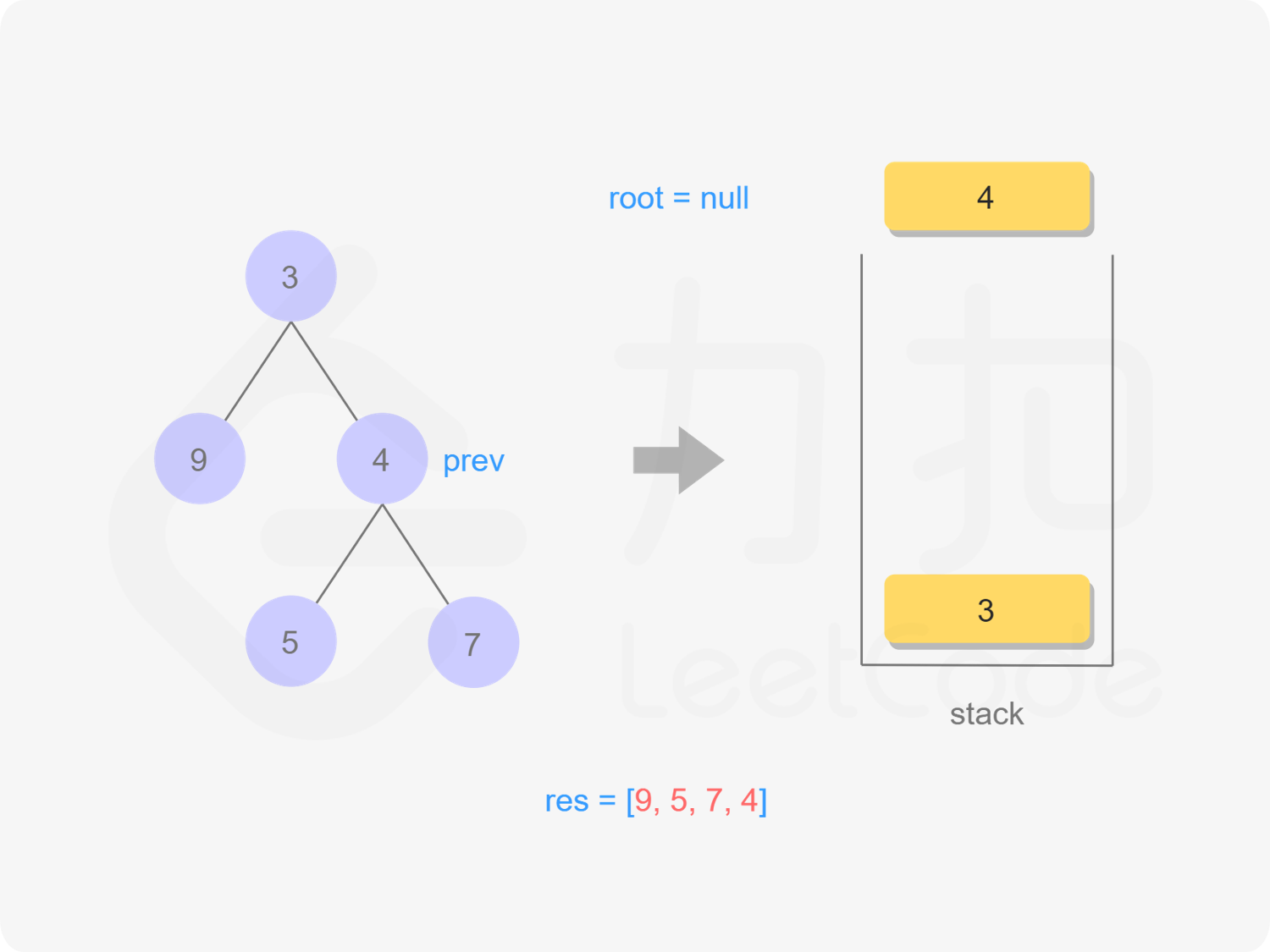
"图18"

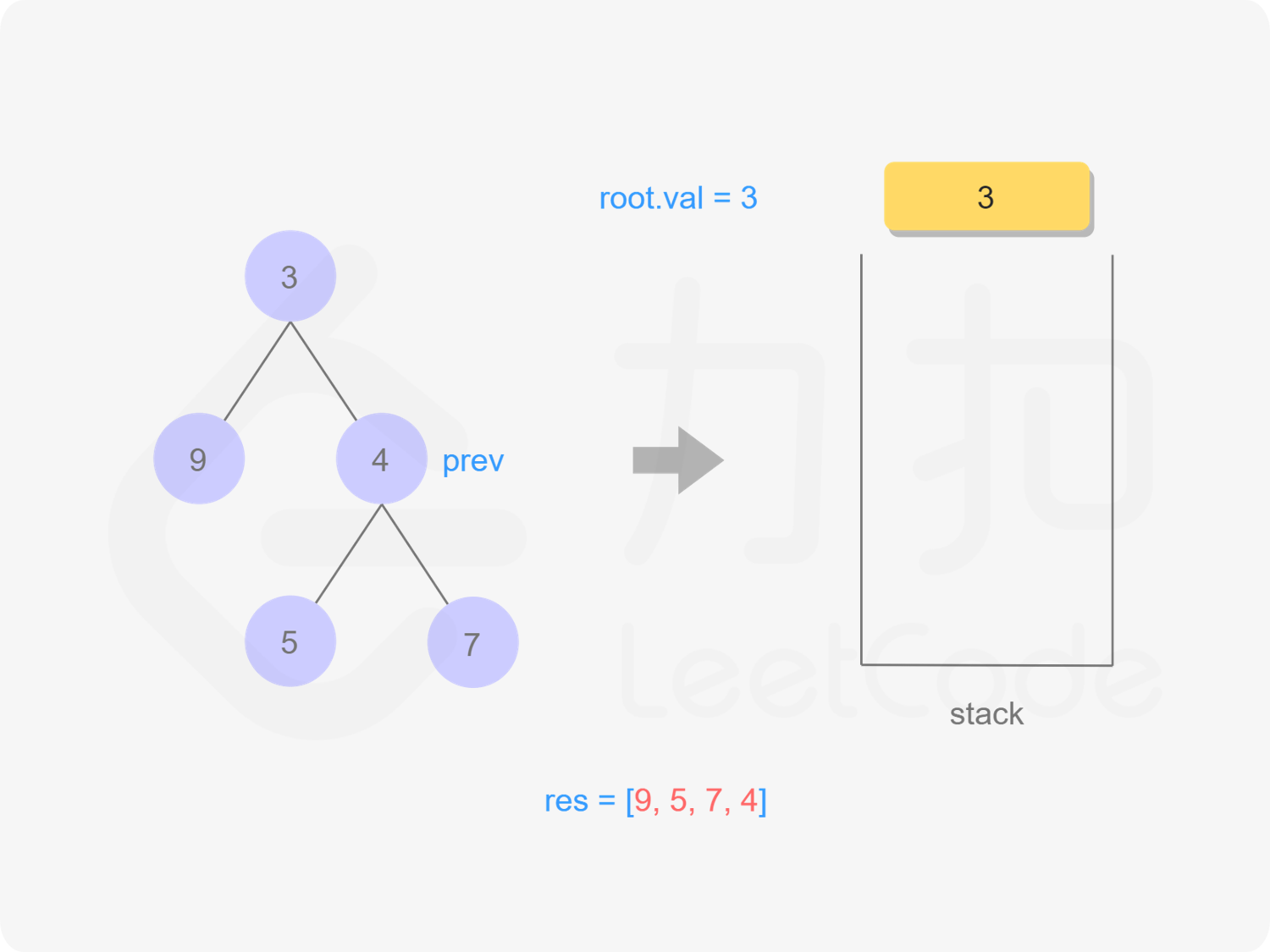
"图19"

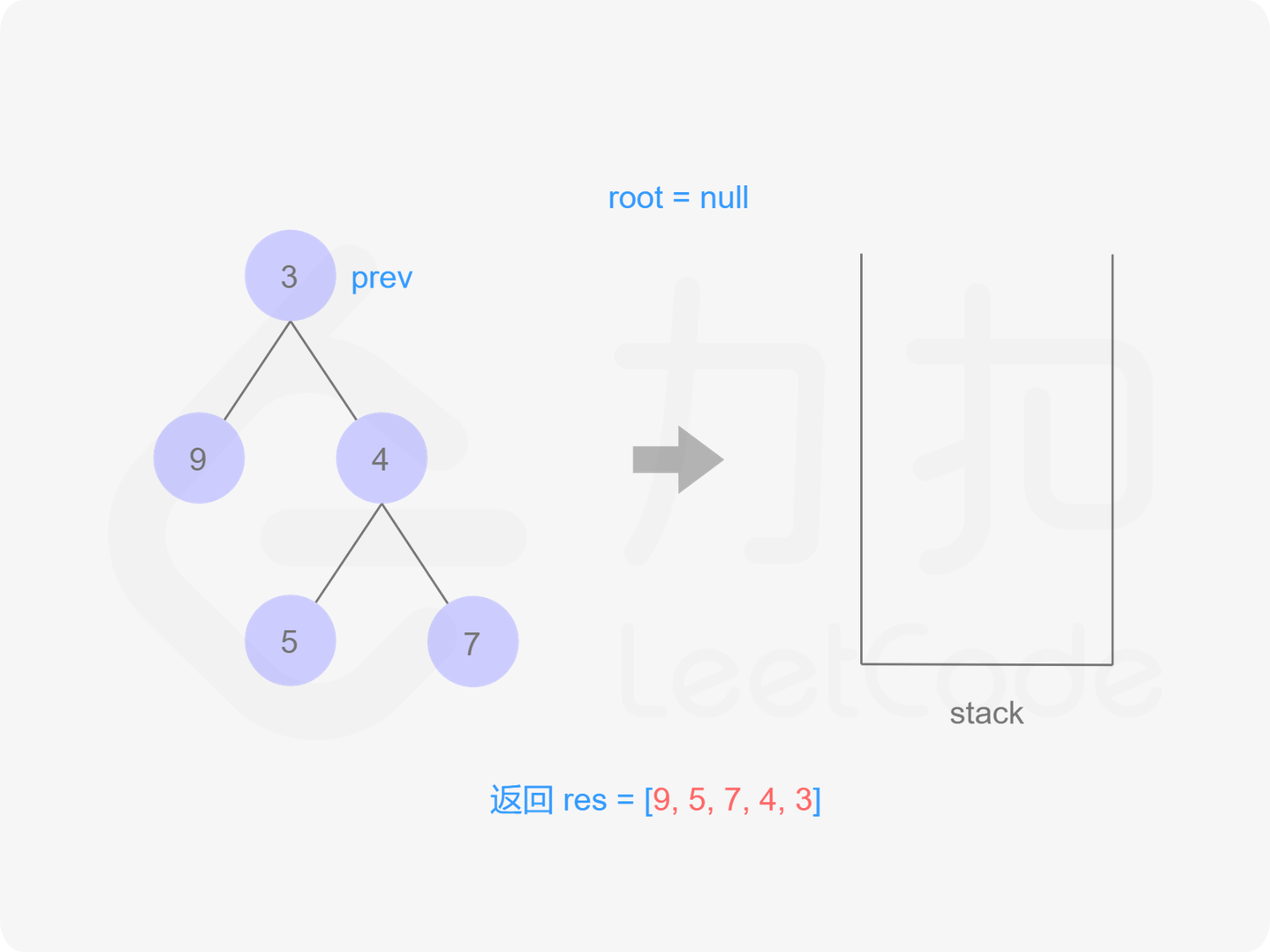
"图20"

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

3.代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
	//迭代
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (null == root) {
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode prev = null;
        TreeNode current = root;
        while (null != current || !stack.isEmpty()) {
            while (null != current) {
                stack.push(current);
                current = current.left;
            }
            //获取当前栈顶节点
            current = stack.peek();
            //右节点为空，或者已经访问过，则打印，并标记当前出栈的节点为已访问过
            if (null == current.right || prev == current.right) {
                res.add(current.val);
                prev = current;
                stack.pop();
                current = null;
            } else {
                current = current.right;
            }
        }
        return res;
    }
	
	//递归
	public int[] postorderTraversal2 (TreeNode root) {
        if (null == root) {
            return new int[0];
        }
        List<Integer> list = new ArrayList<Integer>();
        postorderTraversal2(list, root);
        return list.stream().mapToInt(Integer::valueOf).toArray();
    }
 
    public void postorderTraversal2 (List<Integer> list, TreeNode root) {
        if (null == root) {
            return;
        }
        postorderTraversal2(list, root.left);
        postorderTraversal2(list, root.right);
        list.add(root.val);
    }
}