【LeetCode】199.二叉树的右视图

1.问题

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1

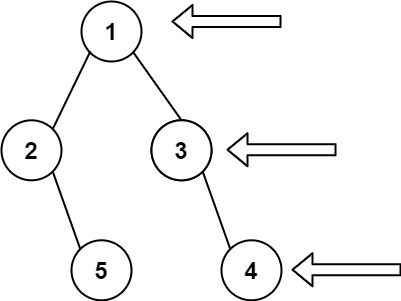
示例

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2

输入: [1,null,3]
输出: [1,3]

示例 3

输入: []
输出: []

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100

  2.解题思路

  经历过前面几篇关于二叉树的层序遍历算法之后（参见【LeetCode】102.二叉树的层序遍历，非常容易的就可以通过这种算法解答此题，基本思想就是围绕队列性质，广度优先算法解决。当然，深度优先算法也是可以解决的。

2.1 广度优先（BFS）

利用队列，遍历每层节点，并记录每层最后一个元素，直到遍历完最后一层，即可得到结果。访问顺序如下图所示：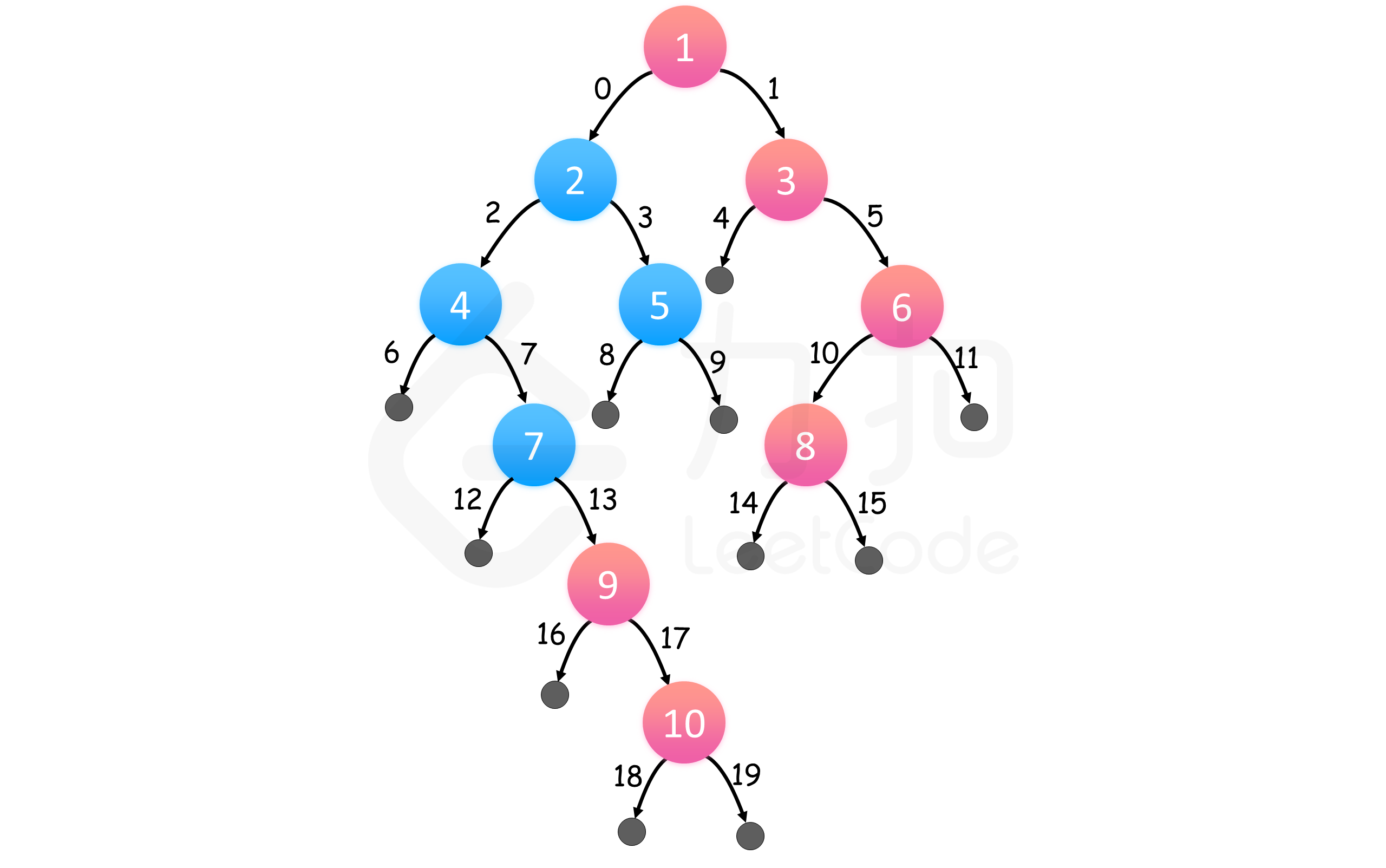

BFS

红色结点自上而下组成答案，边缘以访问顺序标号。
复杂度：

• 时间复杂度： O(N)，每个节点都入队出队了 1 次。
• 空间复杂度： O(N)，使用了额外的队列空间。

  2.2 深度优先（DFS）

  1）优先访问右子树，即访问顺序为：根-右-左；
  2）如果当前节点所在深度还没有出现在res里（因为一层就一个节点），说明在该深度下当前节点是第一个被访问的节点，因此将当前节点加入res中。

  if len(res) < depth:
      res.append(root.val)
  # 遍历右子树
  if root.right:
      dfs(root.right, depth + 1, res)
  # 遍历左子树
  if root.left:
      dfs(root.left, depth + 1, res)

  复杂度：
• 时间复杂度： O(N)，每个节点都访问了 1 次。
• 空间复杂度： O(N)，因为这不是一棵平衡二叉树，二叉树的深度最少是 logN, 最坏的情况下会退化成一条链表，深度就是N，因此递归时使用的栈空间是 O(N) 的。

  3.代码

  /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      /**
      	广度优先
          1.利用层序遍历思想，统计每层最后一个元素，即为答案
          2.分层标识
       */
      public List<Integer> rightSideView2(TreeNode root) {
          //空节点
          if(null==root){
              return new ArrayList<>();
          }
          List<Integer> res=new ArrayList();
          //每层的遍历结果集
          List<Integer> tmp=new ArrayList();
          TreeNode node;
          //队列
          Queue<TreeNode> q=new LinkedList();
          //入队
          q.add(root);
          //分层标识
          q.add(null);
  
          while(!q.isEmpty()){
              node=q.poll();
              if(null!=node){
                  tmp.add(node.val);
                  //左右子树入队
                  if(null!=node.left){
                      q.add(node.left);
                  }
                  if(null!=node.right){
                      q.add(node.right);
                  }
              }
              //否层，该层遍历完毕
              else{
                  if(!tmp.isEmpty()){
                      //收集每层最后一个元素
                      res.add(tmp.get(tmp.size()-1));
                      tmp=new ArrayList();
                      q.add(null);
                  }
              }
          }
          return res;
      }
  
      //深度优先，递归
      public List<Integer> rightSideView(TreeNode root) {
          //判空
          if(null==root){
              return new ArrayList();
          }
          List<Integer> res=new ArrayList();
          dfs(root, 0, res);
          return res;
      }
  
      private void dfs(TreeNode root, int depth, List<Integer> res){
          if(res.size()==depth){
              res.add(root.val);
          }
          //左右子树，先遍历右子树，然后左子树
          if(null!=root.right){
              dfs(root.right, depth+1, res);
          }
          if(null!=root.left){
              dfs(root.left, depth+1, res);
          }
      }
  }