【LeetCode】404. 左叶子之和

1.问题

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1

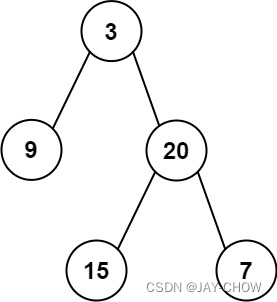
"图1"

输入: root = [3,9,20,null,null,15,7]
输出: 24

解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2

输入: root = [1]
输出: 0

提示:

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

2.解题思路

2.1 递归

按照题目描述，我们需要遍历每个树节点，对于目标值，我们需要判定某个节点是否是需要的，既要判定是叶子节点，又要判定是左边的叶子节点，因而对于和的组成，进行分类谈论，如下：
1）节点为null，返回；
2）该节点左子树不为空，且为叶子节点，sum+=该节点的value；否则递归左子树；
3）该节点右子树不为空，这里又要分类：
3.1）右子树为叶子节点，不是题目需要的值的组成部分；
3.2）右子树的子节点，只要左右其中一个不为空，继续递归。

伪代码：

//sumOfLeftLeaves(TreeNode root)为计算root所有左叶子节点的和的函数。
int sumOfLeftLeaves(TreeNode root){
	//节点为null
	if root 为null
		return 0;
	//左子树
	if root.left 不为null
		//root.left为叶子节点
		if(root.left为叶子节点){
			sum+=root.left.val;
		}
		//否则，继续递归左子树
		else {
			sum+=sumOfLeftLeaves(root.left);
		}
	
	//右子树
	if root.right 不为null
		//只要不是叶子节点，继续递归
		if root.right 不是叶子节点
		 sum+=sumOfLeftLeaves(root.right);
	return sum;
}

而判定是否是叶子节点，代码如下：

//判定是叶子节点
private boolean isLeaf(TreeNode node){
    return null!=node && null==node.left && null==node.right;
}

2.2 改进的递归

上述递归流程，过程是清晰明了的，但判定逻辑有点复杂，对于题目已知的条件，我们只需要抓重点，左叶子节点的和，其他都放在递归算法里了。
详细代码，见第3节代码。

2.3 BFS

前面讨论的算法，遍历路径类似前序遍历，先根节点，再左右子节点，本质思想还是深度优先（DFS）。在二叉树遍历系列文章中，我们可以利用层序遍历，同样可以解决本章问题，其思想还是广度优先算法（BFS）。

3.代码

3.1 递归算法

public int sumOfLeftLeaves2(TreeNode root) {
   if(null==root){
       return 0;
   }
   int sum=0;
   if(null!=root.left){
       //左子树为叶子节点，直接加上，否则继续递归左子树
       if(isLeaf(root.left)){
           sum+=root.left.val;
       }else {
           sum+=sumOfLeftLeaves(root.left);
       }
   }
   //右子树只要不为空，且至少存在一个节点（不管是左还是右）
   if(null!=root.right){
       if(!isLeaf(root.right)){
           sum+=sumOfLeftLeaves(root.right);
       }
   }
   return sum;
}

3.2 改进的递归

int sum=0;
public int sumOfLeftLeaves(TreeNode root) {
    dfs(root);
    return sum;
}

private void dfs(TreeNode root){
    if(null==root){
        return;
    }
    //是左叶子节点
    if(null!=root.left && isLeaf(root.left)){
        sum+=root.left.val;
    }
    //继续遍历左右子树
    dfs(root.left);
    dfs(root.right);
}

3.3 广度优先算法

public int sumOfLeftLeaves(TreeNode root) {
   if(null==root){
       return 0;
   }
   int sum=0;
   //队列
   Queue<TreeNode> q=new LinkedList<>();
   q.offer(root);
   TreeNode node;
   //遍历队列
   while(!q.isEmpty()){
       node=q.poll();
       if(null==node){
           continue;
       }
       //左叶子节点
       if(null!=node.left && isLeaf(node.left)){
           sum+=node.left.val;
       }
       q.offer(node.left);
       q.offer(node.right);
   }
   return sum;
}