1 问题
给定一个可包含重复数字的序列 nums ,按任意顺序返回所有不重复的全排列。
示例 1
- 输入:nums = [1,1,2]
- 输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
2 解题思路
可参考上一篇文章中提到的回溯法解决。主要区别在于此题中的数组包含重复数字。因而,在回溯开始之前,对数组nums进行排序。
在for循环中,对于重复、未使用的的数字要进行排除,即跳过此次循环。
for(int i=0;i<nums.length;i++){
if(used[i]){
continue;
}
//去重最为关键的代码。
if(i>0 && nums[i-1]==nums[i]&& !used[i-1]){
continue;
}
}也可以是这样:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) {
continue;
}为啥子?
used[i - 1] == false或者!used[i-1]属于树层上的去重used[i-1] == true或者used[i-1]属于树枝上的去重
比如:[1,1,1]
树层上去重(used[i - 1] == false),的树形结构如下: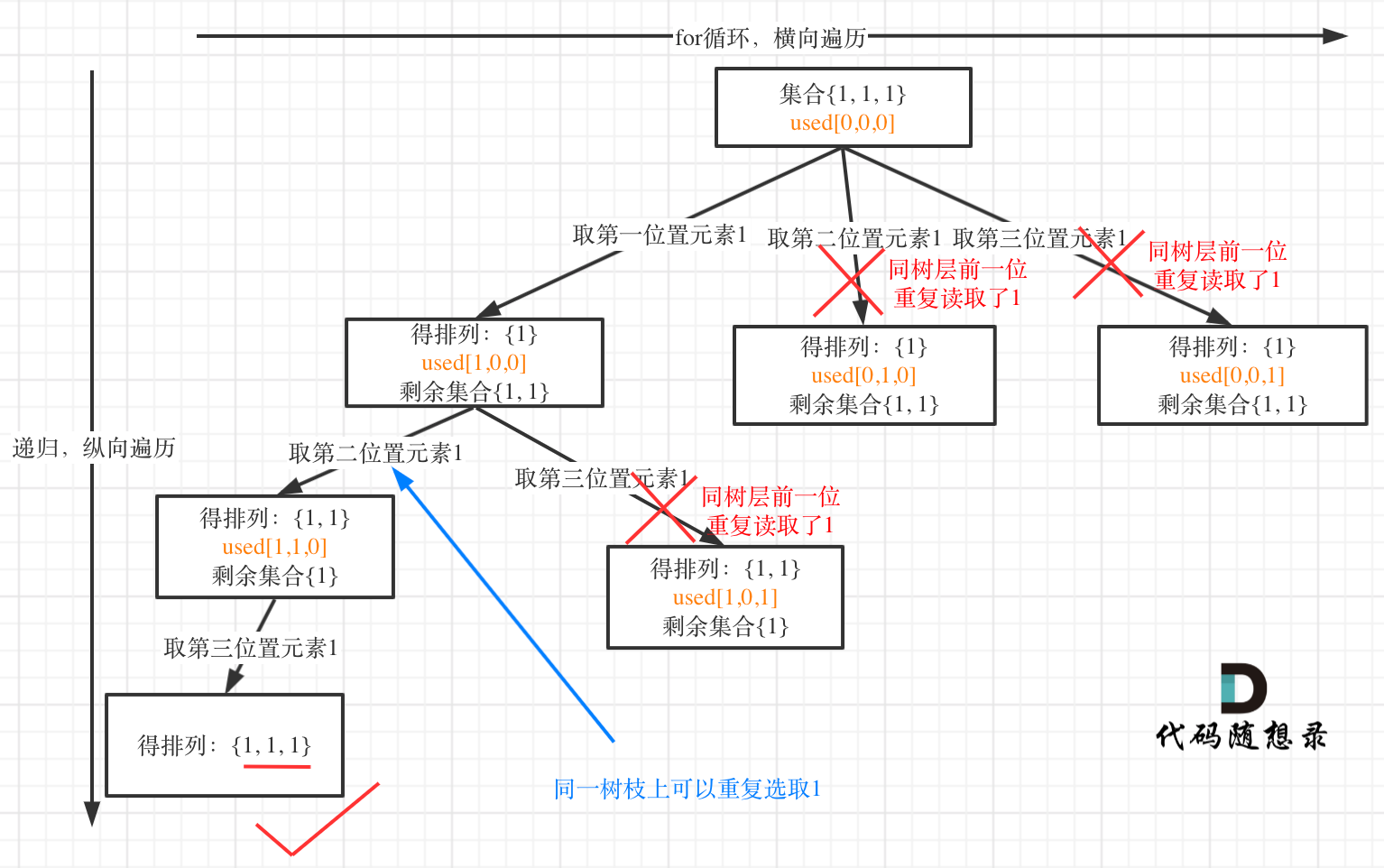
树枝上去重(used[i - 1] == true)的树型结构如下: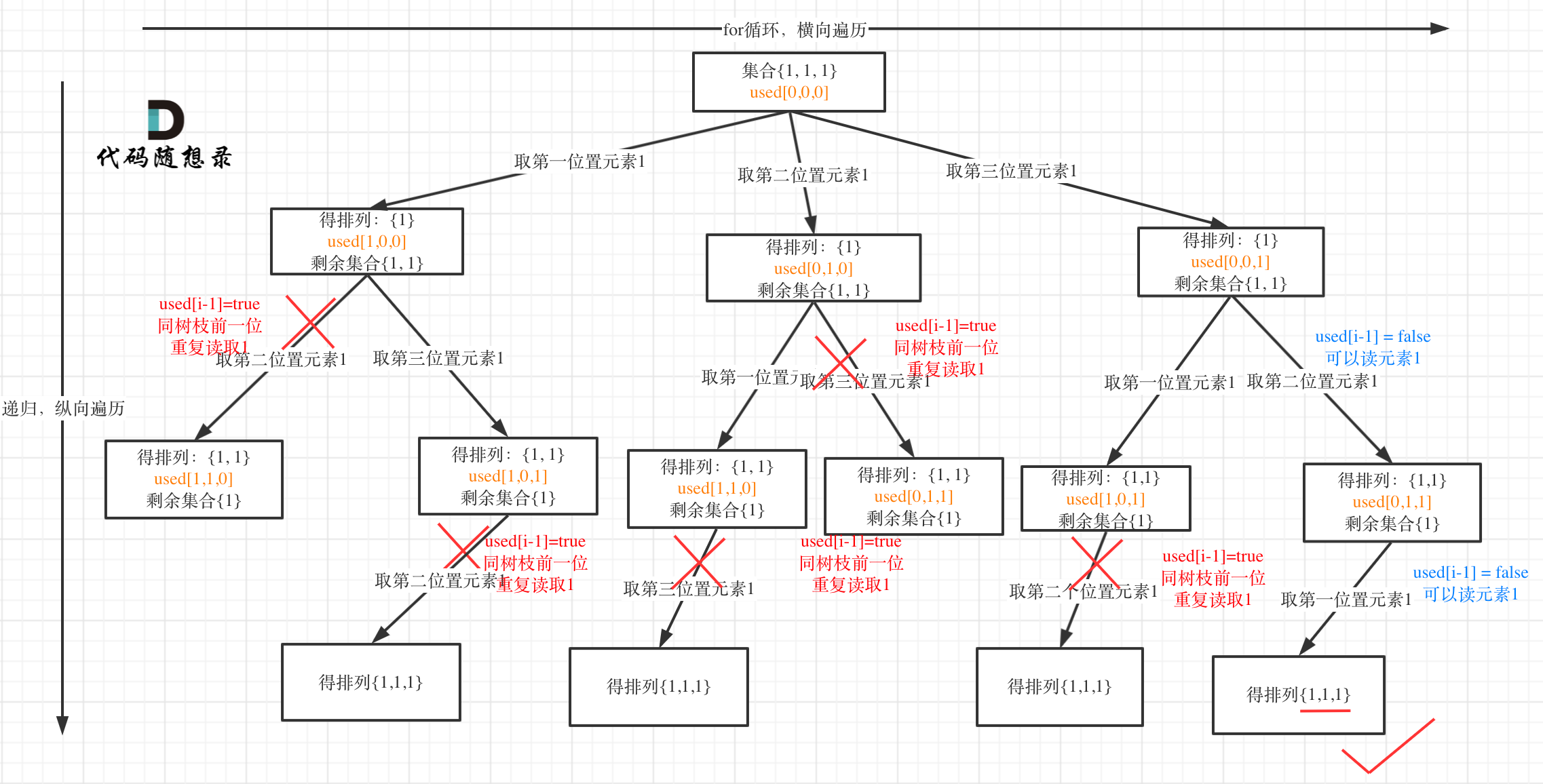
具体参考录哥 的思路。这是🐂🍺。
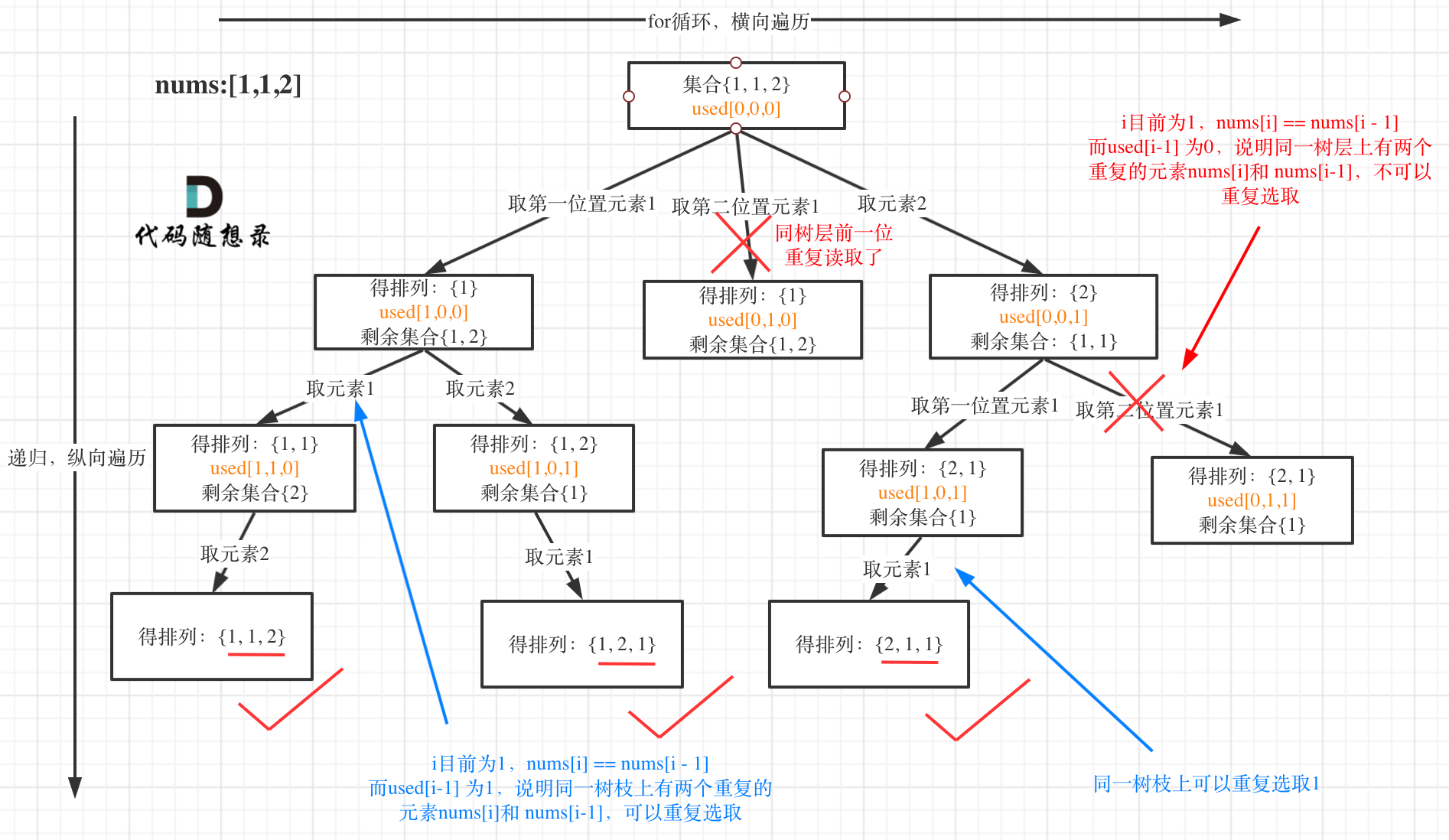
3 代码
class Solution {
//结果集
List<List<Integer>> res=new LinkedList<>();
//临时结果
LinkedList<Integer> track=new LinkedList<>();
//是否已使用
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
used=new boolean[nums.length];
//题目中有重复数字可用,那就先排序,把相同的放一起
Arrays.sort(nums);
backtrace(nums);
return res;
}
private void backtrace(int[] nums){
if(track.size()==nums.length){
res.add(new LinkedList(track));
return;
}
for(int i=0;i<nums.length;i++){
if(used[i]){
continue;
}
//去重最为关键的代码。至于是利用 !used[i-1],还是 used[i-1],参考:https://leetcode.cn/problems/permutations-ii/solutions/418230/47-quan-pai-lie-iiche-di-li-jie-pai-lie-zhong-de-q/
if(i>0 && nums[i-1]==nums[i]&& !used[i-1]){
continue;
}
used[i]=true;
track.add(nums[i]);
backtrace(nums);
//剔除当前选择
track.removeLast();
used[i]=false;
}
}
}


