1 问题
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3
输入:nums = [1]
输出:[[1]]
提示:
- 1 <= nums.length <= 6
- -10 <= nums[i] <= 10
- nums 中的所有整数
互不相同
2 解题思路
2.1 回溯法
本题给定的条件是:不重复的数字、全排列,根据数学中的排列组合公式,全排列的个数有 n!,其中n为数组元素个数。
2.1.1 基本公式(伪代码)
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择- 路径:已经做出的选择。
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
2.1.2 核心思想
for 循环里面的递归,在递归调用之前
做选择,在递归调用之后撤销选择。
在for循环中,我们引入一个boolean数组,用于记录数组中各位是否使用,即是否已经选择了某个元素。做出选择,标记为true;取消选择,标记为false。
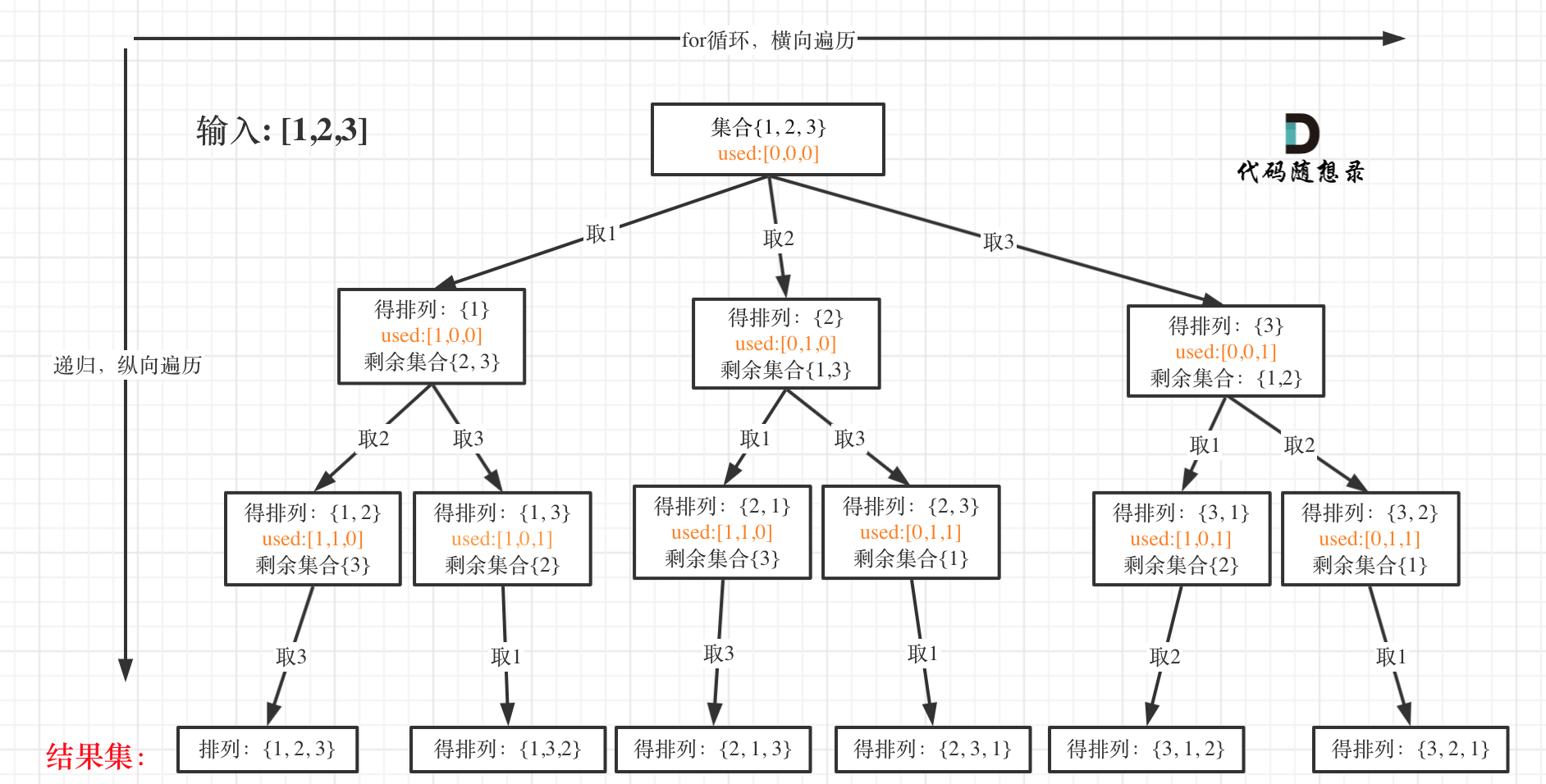
2.2 迭代(插空法)
详见这位大神的解法。
3 代码
class Solution {
List<List<Integer>> res=new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
LinkedList<Integer> track=new LinkedList<>();
// 「路径」中的元素会被标记为 true,避免重复使用
boolean[] used = new boolean[nums.length];
backtrack(nums, track, used);
return res;
}
/**
* 回溯:
* @param track 路径:记录在 track 中
* @param nums-选择列表:nums 中不存在于 track 的那些元素
* 结束条件:nums 中的元素全都在 track 中出现
*/
private void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used){
if(track.size()==nums.length){
res.add(new LinkedList(track));
return;
}
//遍历
for(int i=0;i<nums.length;i++){
//已经使用过了,跳过该数字
if(used[i]){
continue;
}
used[i]=true;
//选择,加入该数字
track.add(nums[i]);
//进入下一层
backtrack(nums, track, used);
//取消选择
track.removeLast();
//恢复该数字为 未使用
used[i]=false;
}
}
}

