1 问题
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是(i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1

输入:[1,8,6,2,5,4,8,3,7]
输出:49
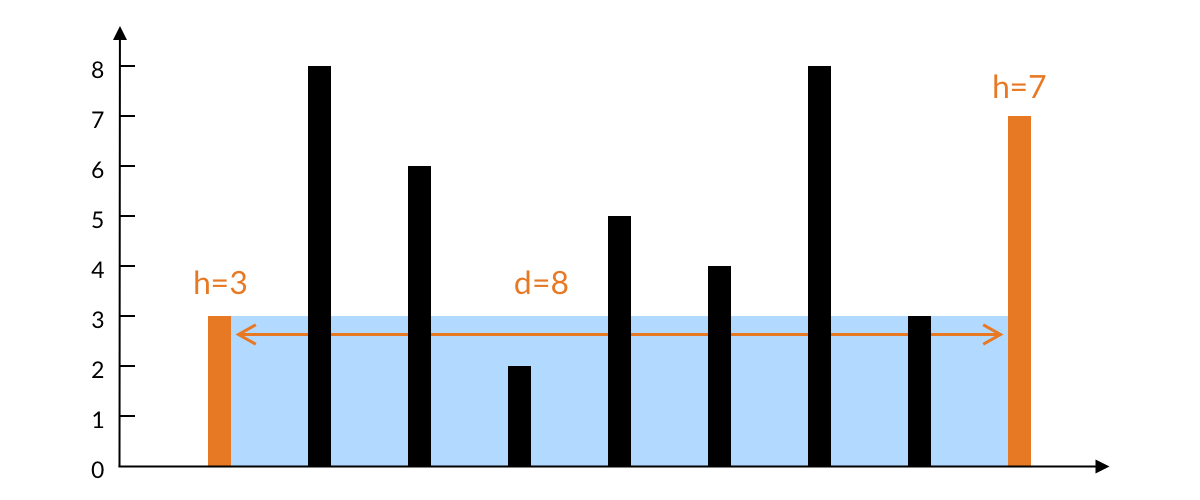
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2
输入:height = [1,1]
输出:1
提示:
- n == height.length
- 2 <= n <= 105
- 0 <= height[i] <= 104
2 解题思路
2.1 双指针
转自Krahets
设两指针 left , right ,指向的水槽板高度分别为 $h{left}$,$h{right}$,此状态下水槽面积为 $S_{ij}$ 。由于可容纳水的高度由两板中的 短板 决定,因此可得如下面积公式 :
$S{ij}$ = (right-left)*Min($h{left}$,$h_{right}$)
- 算法流程:
- 初始化: 双指针
left,right分列水槽左、右两端; - 循环收窄: 直至双指针相遇时跳出;
- 更新面积最大值
res; - 选定两板高度中的
短板,向中间收窄一格; - 返回值: 返回面积最大值 res 即可;
- 初始化: 双指针
3 代码
class Solution {
public int maxArea(int[] height) {
//双指针
//容量:(right-left)*Min(height[left], height[right])
int left=0;
int right=height.length-1;
int res=0;
int s;
while(left<right){
s=(right-left)*Math.min(height[left], height[right]);
res=Math.max(res, s);
if(height[left]<height[right]){
left++;
}
else {
right--;
}
}
return res;
}
}

